[Medium] 53. Maximum Subarray (아마존 코딩 테스트 기출 문제)

#문제 설명

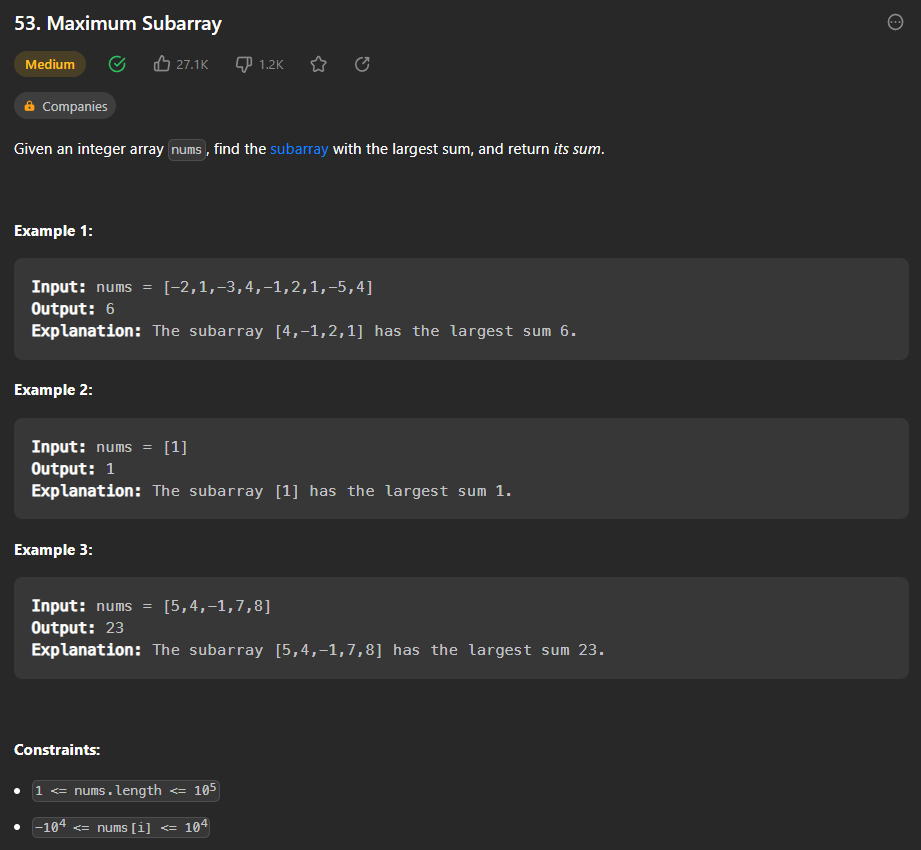
Leetcode 53번 문제는 정수형 배열이 있을 때, 그 배열의 subarray 즉, 부분 배열(주어진 배열의 연속한 일부분) 중 각 원소의 합이 가장 큰 부분 배열을 찾는 문제이다. 여기서 subarray란 주어진 배열에서 끊기지 않고 인접한 원소들의 집합이다. 예를 들어 [1,2,3,4,5]라는 배열에서 subarray는 [1,2], [2,3,4] 등등이 될 수 있다. 하지만 [1,3,5] 같이 인접하지않는 원소들로 구성된 배열은 subarray라고 할 수없다.   

#문제 풀이

class Solution {
    public int maxSubArray(int[] nums) {
        int currSum = 0; 
        int maxSum = Integer.MIN_VALUE;

        for(int i = 0; i < nums.length;i++){
            currSum = Math.max(nums[i], currSum + nums[i]);
            maxSum = Math.max(maxSum, currSum);
        }
        return maxSum;
    }
}

이 문제의 가장 쉬운 풀이는 Kadane's Algorithm (카데인 알고리즘)을 사용한 풀이 이다. 풀이 방법을 굉장히 간단하다. 먼저, 현재의 합을 계산하는 변수(currSum)와 최대값을 계산하는 변수(maxSum)를 만든다. 그 다음 주어진 array를 iterate하면서 만약 currSum을 현재 index의 값, 즉, nums[i] 또는 currSum + nums[i]중에 더 큰 수를 고른다. 만약 [-2,1,-3,4,-1,2,1,-5,4]의 array가 주어졌다고 할때 처음 currSum의 값은 -2가 되고, index 1에 도달하면 currSum의 값은 1이 될 것이다. 왜냐하면 처음 currSum의 값은 -2였고, 1 (nums[i])의 값이 -2 + 1 = -1 (currSum + nums[i])의 값보다 크기 때문이다. 그 다음 만약 currSum의 값이 maxSum보다 클시 maxSum의 값을 currSum의 값으로 업데이트 해준다. 

 

#Divide and Conquer 풀이

class Solution {
    public int maxSubArray(int[] nums) {
        return findMaxSum(nums, 0, nums.length-1);     
    }
    
    private int findMaxSum(int[] nums, int s, int e){
        if(s==e) return nums[s];
        
        int mid = s + (e-s)/2;
        
        int leftMax = findMaxSum(nums, s, mid);
        int rightMax = findMaxSum(nums, mid+1, e);
        int arrMax = findMaxCrossSum(nums, s, mid, e);
      
        
        return Math.max(leftMax, Math.max(rightMax, arrMax));
    }
    
    private int findMaxCrossSum(int []nums, int s, int m, int e){

        int lSum=0, lMax=Integer.MIN_VALUE;
		
        for(int i=m; i>=s; i--){
            lSum+=nums[i];
            lMax = Math.max(lMax, lSum);        
        }
        
        int rSum=0, rMax=Integer.MIN_VALUE;
		
        for(int i=m+1; i<=e; i++){
            rSum+=nums[i];
            rMax = Math.max(rMax, rSum);
        }
        
        return lMax+rMax;
    }
}