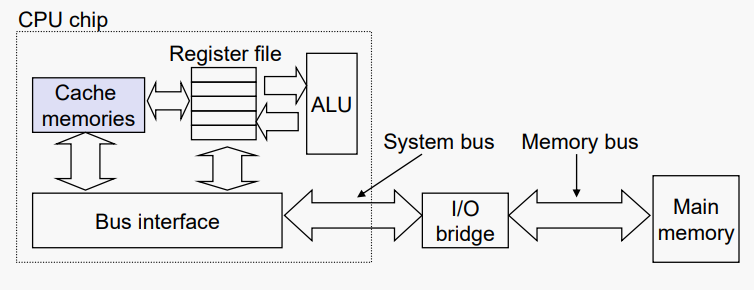
#Cache Memories
- 캐시 메모리는 하드웨어에서 자동으로 관리되는 작고 빠른 SRAM 기반 메모리이다
- 자주 액세스하는 기본 메모리 블록 보유
- CPU는 캐시(예: L1, L2, L3)에서 데이터를 먼저 찾은 다음 메인 메모리에서 데이터를 찾는다
일반적인 캐시 메모리 시스템 구조:
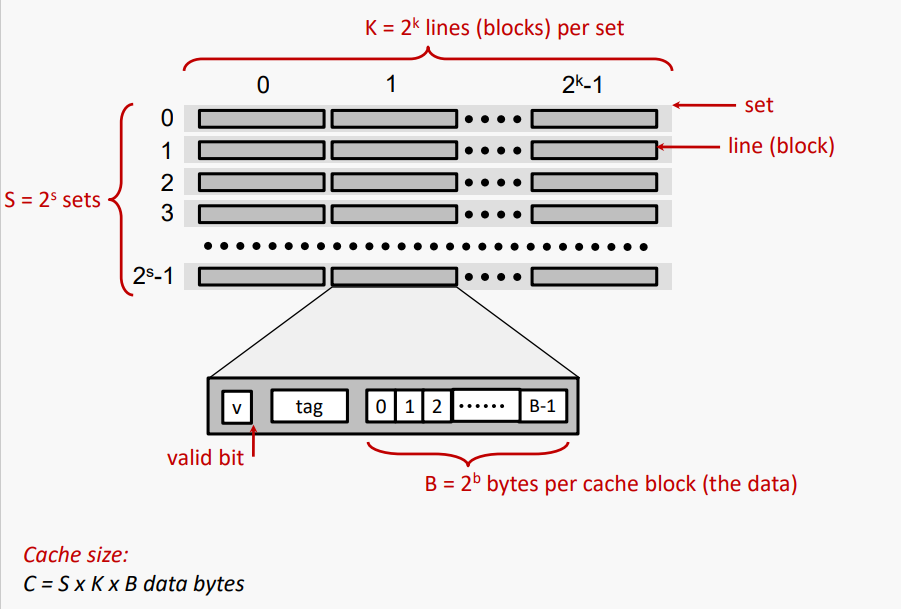
#General Cache Organization (S, K, B)
#Cache Defines View of DRAM
캐시의 "기하학"은 다음과 같이 정의된다
S = 2^s 캐시의 세트 수
K = 2^k 집합의 선(블록) 수
B = 2^b 한 줄의 바이트 수(블록)
이 값들은 DRAM의 구성에 대한 관련 사고 방식을 정의한다
DRAM은 B 바이트의 일련의 블록으로 구성된다. 블록(라인)의 바이트는 b비트를 사용하여 인덱싱할 수 있다.
DRAM은 S 블록(라인) 그룹의 시퀀스로 구성된다. 그룹의 블록(라인)은 비트를 사용하여 인덱싱할 수 있다.
각 그룹에는 SxB 바이트가 포함되어 있으며, s + b 비트를 사용하여 인덱싱할 수 있다.
#Cache (8, 2, 4) and 256-Byte DRAM
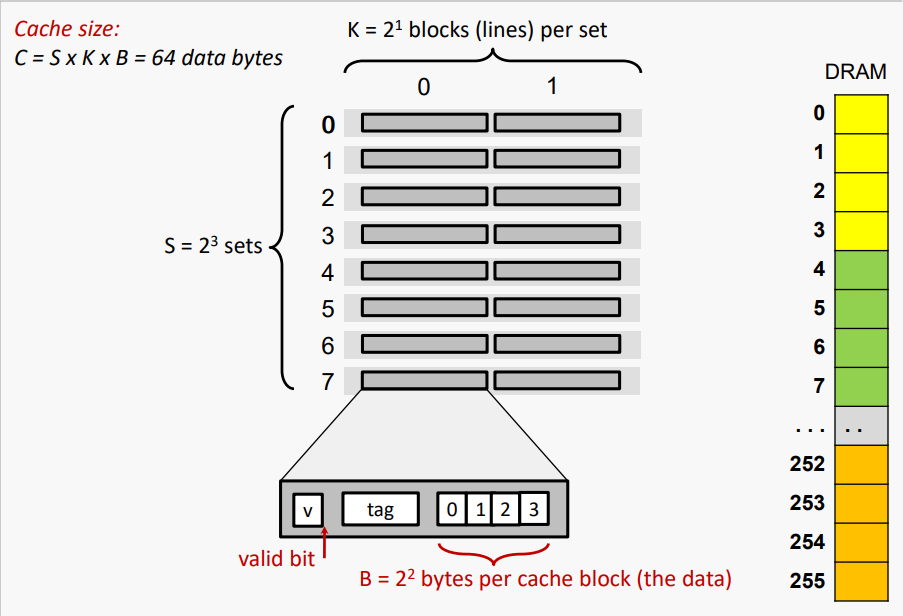
#Cache View of DRAM
그래서, 일반화하자면, 캐시가 다음을 가지고 있다고 가정하자
S = 2^s 개의 세트
K = 2^k 개의 집합당 블록(선)
B = 2^b 개의 블록당 바이트 수
그리고 DRAM이 N비트 주소를 사용한다고 가정하자
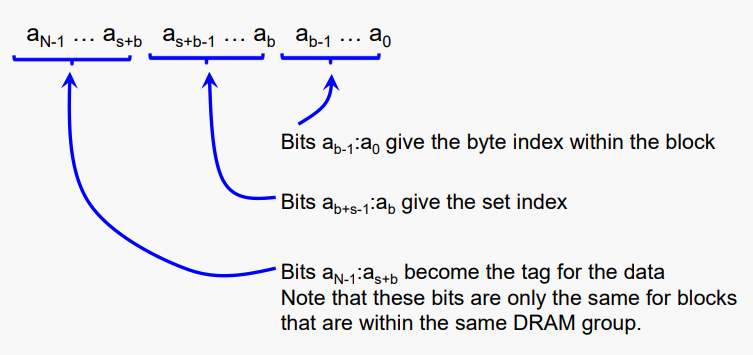
#Cache Read
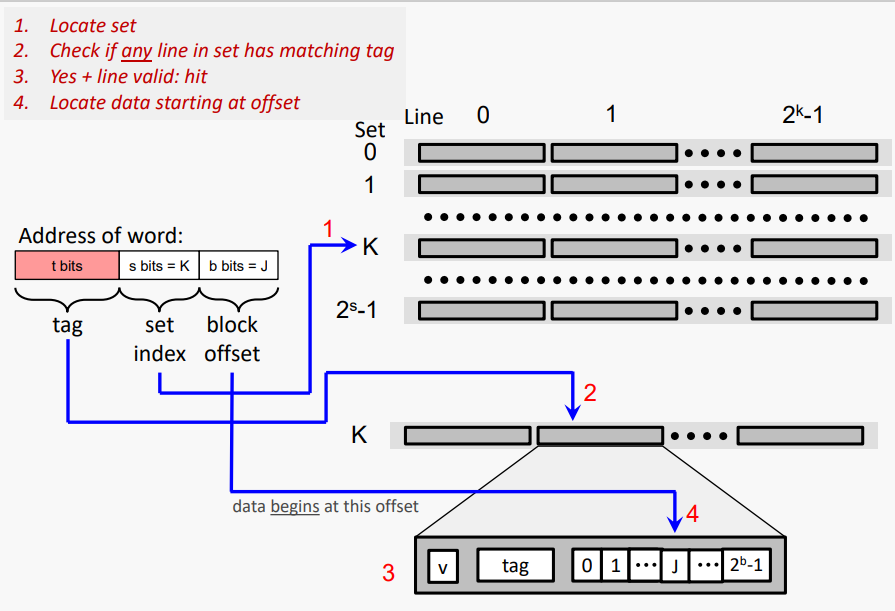
#예시: Direct Mapped Cache (K = 1)
직접 매핑 (Direct mapped): K = 1 / 한 세트당 한 줄
캐시 블록 크기 8바이트로 가정
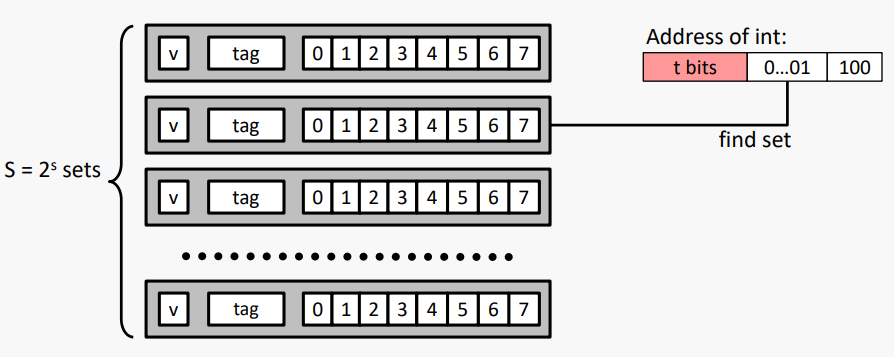
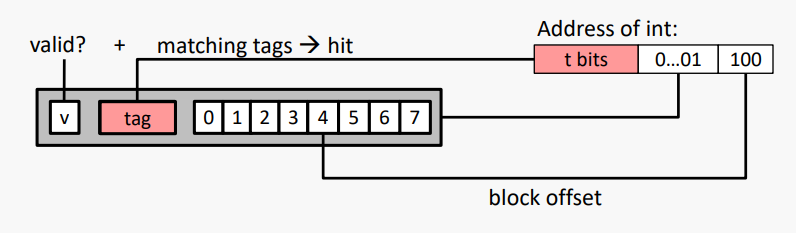
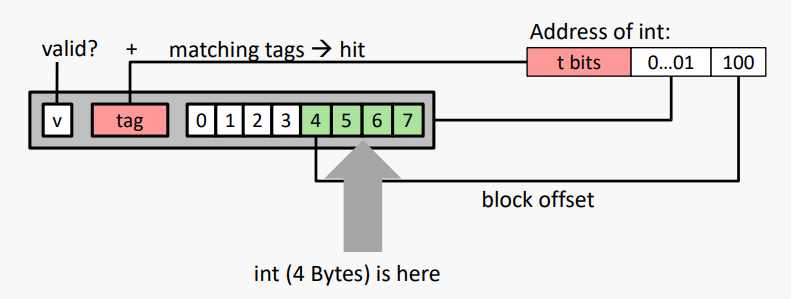
매칭 없음: 이전 라인(블록)이 제거되고 DRAM에서 요청된 블록으로 대체됨
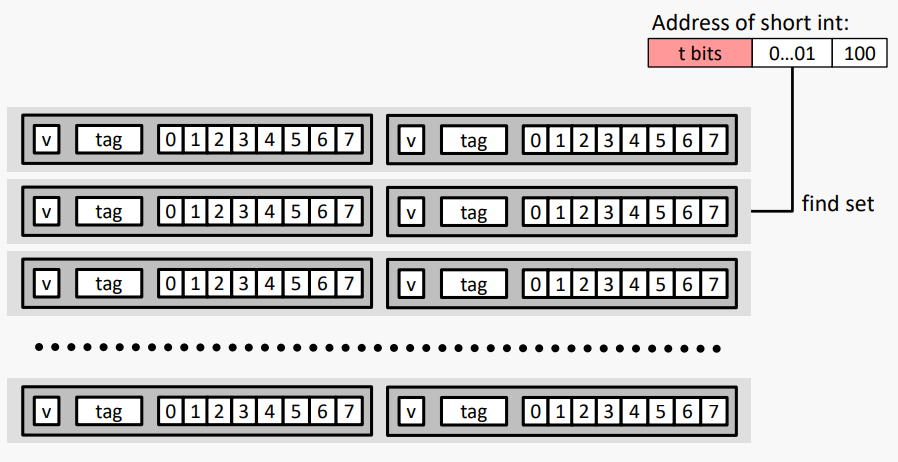
#K-way Set Associative Cache (Here: K = 2)
K = 2: 한 세트당 두 줄
캐시 블록 크기 8바이트로 가정
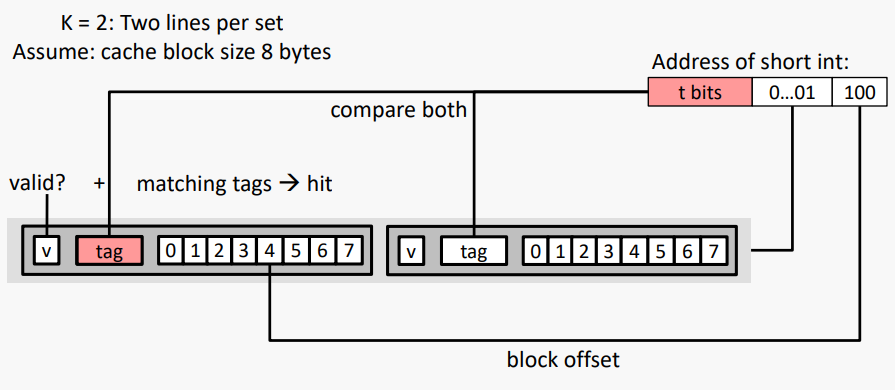
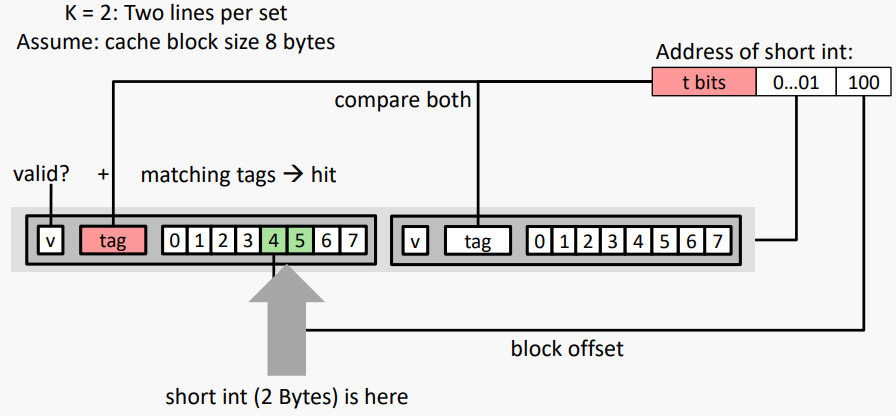
- No match:
- 제거 및 교체를 위해 집합에서 하나의 라인이 선택됨
- Replacement policies: 랜덤 또는 LRU(least recently used)
#Cache Organization Types
위에도 언급했 듯이 캐시의 "기하학"은 다음과 같이 정의된다
S = 2^s 캐시의 세트 수
K = 2^k 집합의 선(블록) 수
B = 2^b 한 줄의 바이트 수(블록)
K = 1 (k = 0) direct-mapped cache: 각 DRAM 블록에 대해 캐시에서 단 하나의 가능한 위치
S > 1 / K > 1 K-way associative cache: 각 DRAM 블록에 대해 K개의 가능한 위치(동일한 캐시 세트 내)
S = 1 (only one set) fully-associative cache: K = 각 DRAM 블록이 캐시의 모든 위치에 있을 수 있는 캐시 블록 수
#Cache Example
5비트 주소(32-word DRAM), Direct-mapped, 8블록, word/블록 1개가 있다고 가정하자
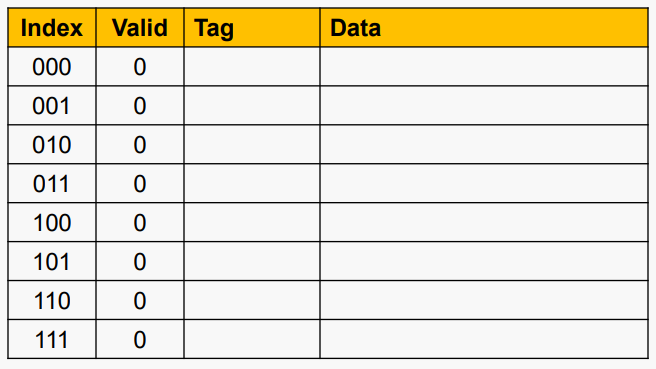
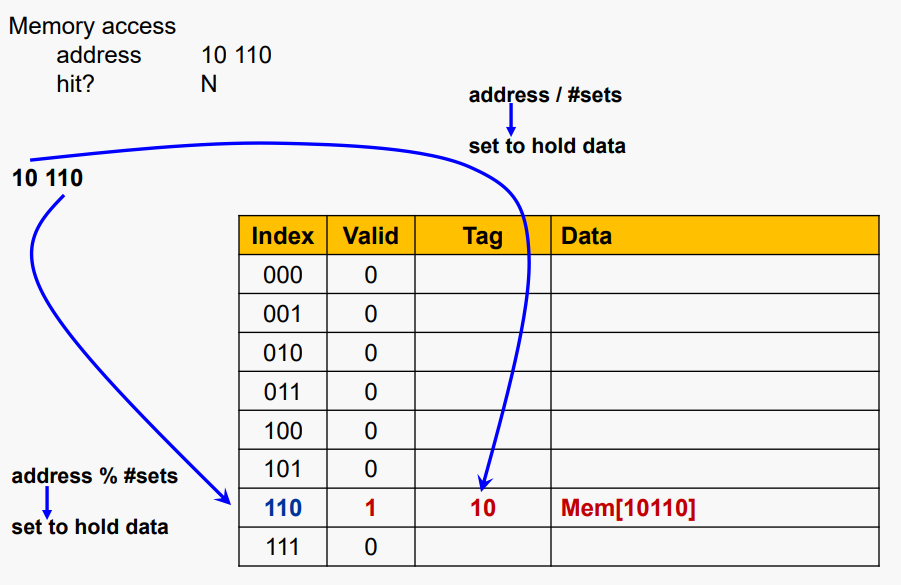
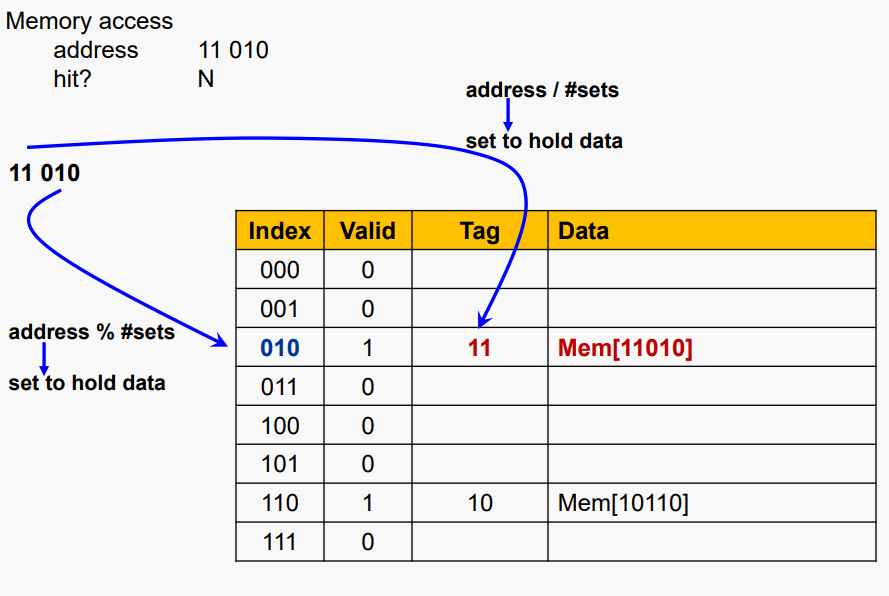
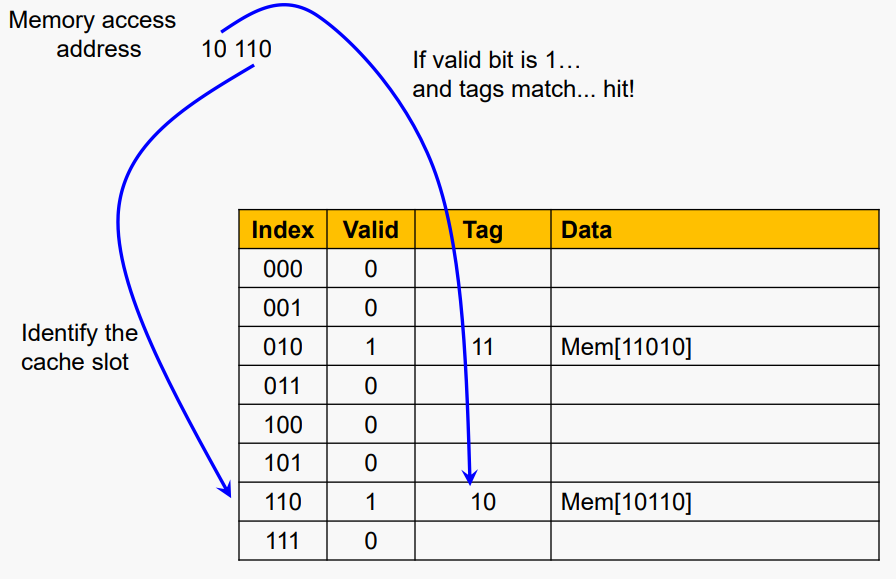
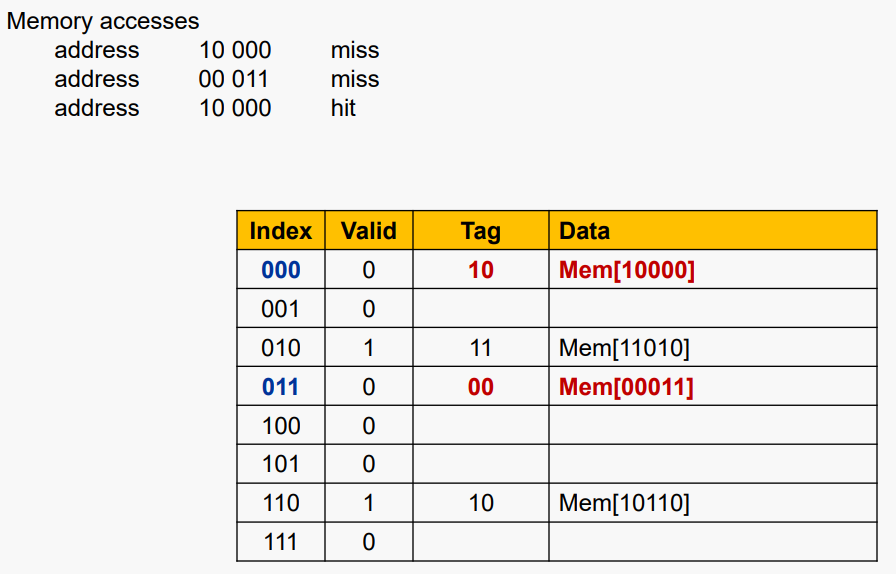
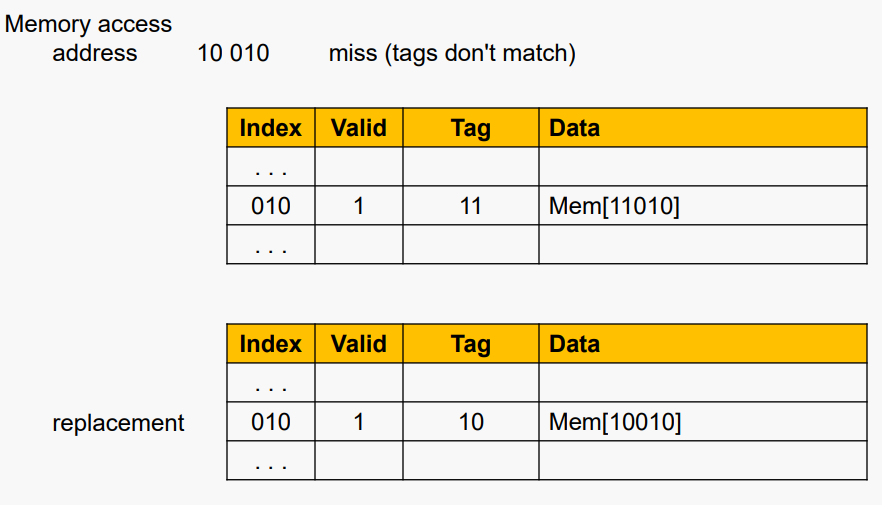
#Block Size Considerations
- 블록이 클수록 miss rate이 감소한다
- 공간 구역성때문
- 그러나 고정된 크기의 캐시에는
- 더 큰 블록 -> miss rate 증가
- 더 많은 경쟁 -> miss rate 증가
- 더 큰 블록 -> pollution
- 더 큰 블록 -> miss rate 증가
- 더 큰 miss 패널티는
- miss rate 감소의 이점을 오버라이드 할 수 있다
- 조기 재시작 및 critical-word-first가 도움이 될 수 있다
#Cache Misses
캐시 hit 시 CPU가 정상적으로 진행됨
- 캐시 miss시:
- CPU 파이프라인을 stall
- 다음 계층 level에서 블록 가져오기
- instruction cache miss
- instruction fetch 재시작
- data cache miss
- 데이터 접근 완료
#Write-Through
- 데이터 write 적중 시 캐시에서 블록만 업데이트할 수 있다
- 하지만 캐시와 메모리가 일치하지 않을 것이다
- Write through: 메모리 업데이트도 함
- 그러나 write가 더 오래 걸린다
- 예를 들어, 기본 CPI = 1, 10%의 명령이 저장되는 경우 메모리에 쓰기에는 100 사이클이 소요
- effective CPI = 1 + 0.1×100 = 11
- 해결책: write 버퍼
- 메모리에 쓰기를 기다리는 데이터를 보유. CPU가 즉시 계속됨
- 쓰기 버퍼가 이미 가득 찬 경우에만 쓰기 중지
#Write-Back
- 대안: 데이터 쓰기 적중 시 캐시에서 블록 업데이트만 하면 된다.
- 각 블록의 오염(dirty) 여부를 추적
- 더티 블록 교체 시
- 메모리에 다시 쓰기
- 쓰기 버퍼를 사용하여 교체 블록을 먼저 읽을 수 있다
#Write-Allocation
쓰기 miss에 대해 어떤 일이 일어나야 할까?
- write-through의 대안:
- miss시 할당: 블록 fetch 해오기
- write around: 블록 fetch 하지 않기
- 프로그램은 종종 읽기 전에 전체 블록을 쓰기 때문(예: initialization)
- write-back에 대해선
- 보통 블록 fetch해옴
#DRAM Supporting Caches
- 기본 메모리에 DRAM 사용
- 고정 너비(예: 1word)
- fixed-width clocked bus로 연결
- 버스 클럭은 일반적으로 CPU 클럭보다 느림
- 캐시 블록 읽기 예제
- 주소 전송을 위한 버스 사이클 1회
- DRAM 액세스당 15회 버스 사이클
- 데이터 전송당 버스 사이클 1회
- 4-word 블록, 1-word-wide DRAM의 경우
- miss penalty = 1 + 4×15 + 4×1 = 65 bus cycles
- bandwidth = 16 bytes / 65 cycles = 0.25 B/cycle
#Measuring Cache Performance
- CPU 시간의 구성 요소
- 프로그램 실행 주기
- 캐시 적중 시간 포함
- 메모리 stall 주기
- 주로 캐시 miss로 인해

#Cache Performance Operation
- 다음이 주어 졌을때
- I-cache miss rate = 2%
- D-cache miss rate = 4%
- miss penalty = 100 cycles
- base CPI (ideal cache) = 2
- 명령당 miss 주기
- I-cache: 0.02 × 100 = 2
- D-cache: 0.36 × 0.04 × 100 = 1.44
실제 CPI = 2 + 2 + 1.44 = 5.44
이상적인 CPU는 5.44/2 = 2.72배 더 빠르다.
#Average Access Time
Hit time은 성능에도 중요하다
Average memory access time (AMAT): AMAT = Hit time + Miss rate × Miss penalty
예시:
다음이 주어졌을 때
1ns 클럭의 CPU,
hit time = 1 사이클,
miss 패널티 = 20사이클,
I-캐시 miss rate = 5%
AMAT는 다음과 같다
AMAT = 1 + 0.05 x 20 = 2ns(명령당 2주기)
#Performance Summary
CPU 성능이 향상되었을 때, miss penalty가 더 중요해짐
기준 CPI 감소하면, 메모리 스톨에 소요되는 시간 비율 증가한다
클럭 속도(rate) 증가시, 메모리 지연이 더 많은 CPU 주기를 고려함
시스템 성능 평가 시 캐시 동작을 무시할 수 없음
#Associative Caches
- Fully associative
- 지정된 블록이 모든 캐시 항목에서 이동하도록 허용
- 모든 항목을 한 번에 검색해야 함
- entry당 comparator (비쌈)
- K-way set associative
- 캐시 집합에 K개의 항목이 포함되어 있다
- 블록 번호는 어떤 집합인지 결정
- (Block number) % (#Sets in cache)
- 주어진 집합의 모든 항목을 한 번에 검색
- K comparators (덜 비쌈)
#Associative Cache 예제
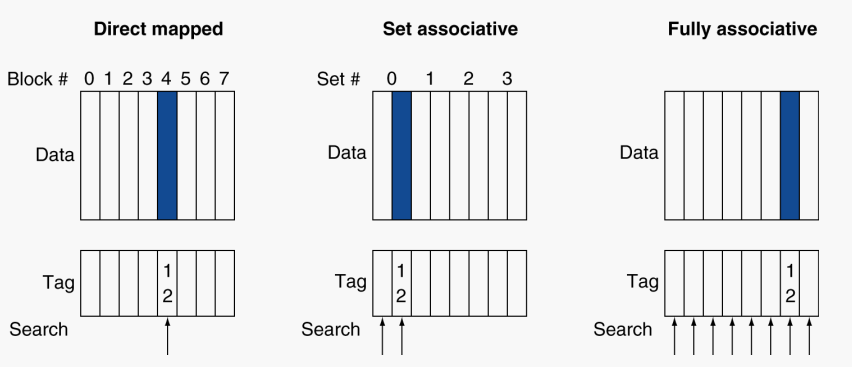
#Spectrum of Associativity
용량: 사용자 데이터 블록 8개

#Associativity 예제
- 4블록 캐시 비교
- 직접 매핑(direct mapped) vs K-way set associative vs ully associative
- 블록 액세스 시퀀스: 0, 8, 0, 6, 8
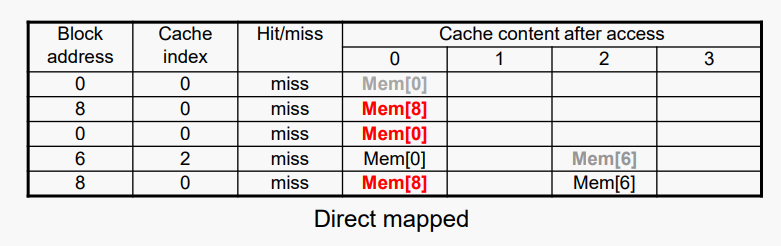
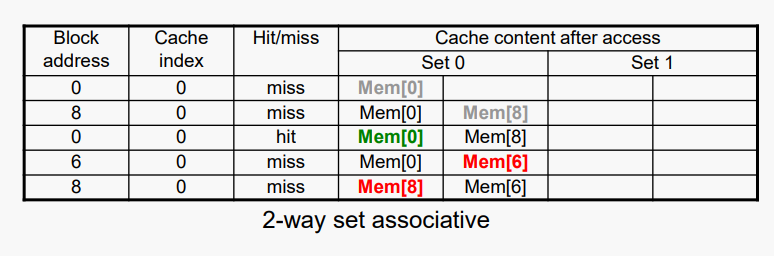
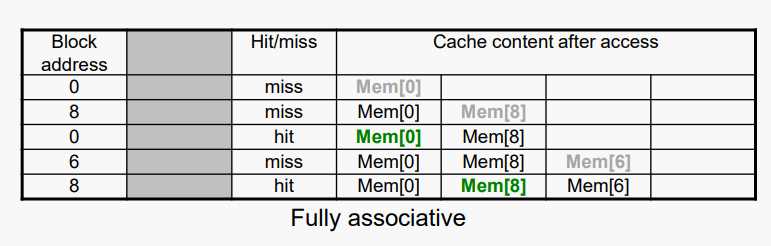
Associativity가 증가하면 miss rate이 감소한다.
- 64KB 시스템 시뮬레이션:
- D-cache, 16-word blocks, SPEC2000
- 1-way: 10.3%
- 2-way: 8.6%
- 4-way: 8.3%
- 8-way: 8.1%
#Set Associative Cache Organization
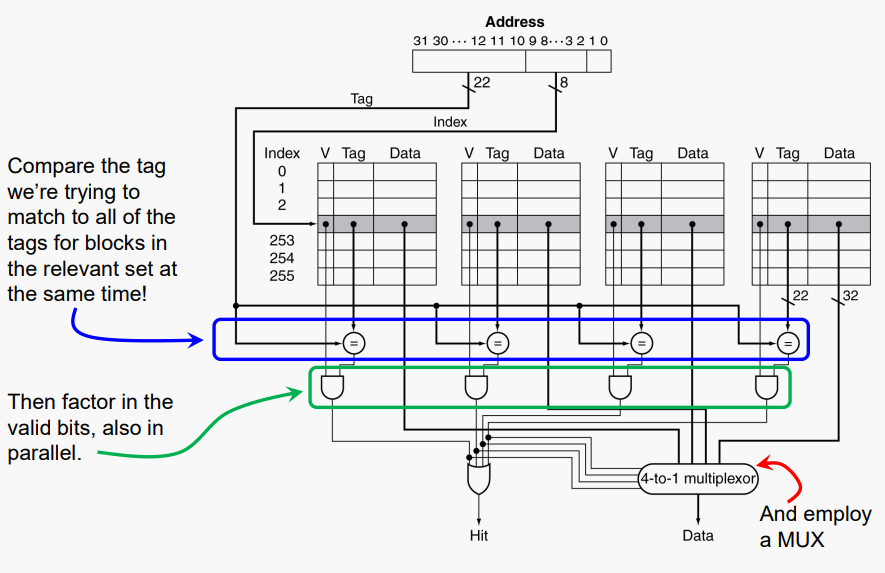
#Replacement Policy
직접 매핑 (Direct mapped): 한 가지 선택만 가능
- Set associative
- 유효하지 않은 항목(non-valid entry)이 있는 경우 해당 항목 선호
- 그렇지 않으면 세트의 항목 중에서 선택
- Least-recently used (LRU)
- 가장 오랫동안 사용하지 않은 것을 고름
- 2-way의 경우 단순하고, 4-way의 경우 관리가 가능, 그 이상은 어려움
- Random
- 높은 연관성을 위해 LRU와 거의 동일한 성능을 제공
#Multilevel Caches
- CPU에 연결된 기본(L-1) 캐시
- 작지만 빠름
- primary 캐시의 레벨 2 캐시 service miss
- 메인 메모리보다 더 크고, 느리지만, 여전히 빠르다
- 메인 메모리 서비스 L-2 캐시
- 일부 하이엔드 시스템에는 L-3 캐시가 포함되어 있다
#Multilevel Cache 예제
- 다음이 주어졌을때
- CPU 기본 CPI = 1, 클럭 속도 = 4GHz
- miss rate/instruction = 2%
- 주 메모리 액세스 시간 = 100ns
- 기본 캐시(primary cache)만 사용했을때
- miss penalty = 100ns / 0.25ns = 400 cycles
- effective CPI = 1 + 0.02 × 400 = 9
- 이제 L-2 캐시 추가
- 액세스 타임 = 5ns
- 기본 메모리에 대한 global miss rate = 0.5%
- L-2 hit 시 1차 miss
- penalty = 5ns / 0.25ns = 20 cycles
- L-2 미스시 1차 미스
- extra penalty = 500 cycles
CPI = 1 + 0.02 × 20 + 0.005 × 400 = 3.4
Performance ratio = 9/3.4 = 2.6
#Multilevel Cache Considerations
- Primary cache
- 최소 적중 시간에 집중
- L-2 cache
- 메인 메모리 액세스를 방지하기 위해 낮은 miss rate에 집중.
- 적중 시간은 전반적인 영향이 적다.
- 결과
- L-1 캐시는 일반적으로 단일 캐시(single monolithic cache)보다 작다.
- L-1 블록 크기가 L-2 블록 크기보다 작다.
#Example: Intel Core i7 Cache
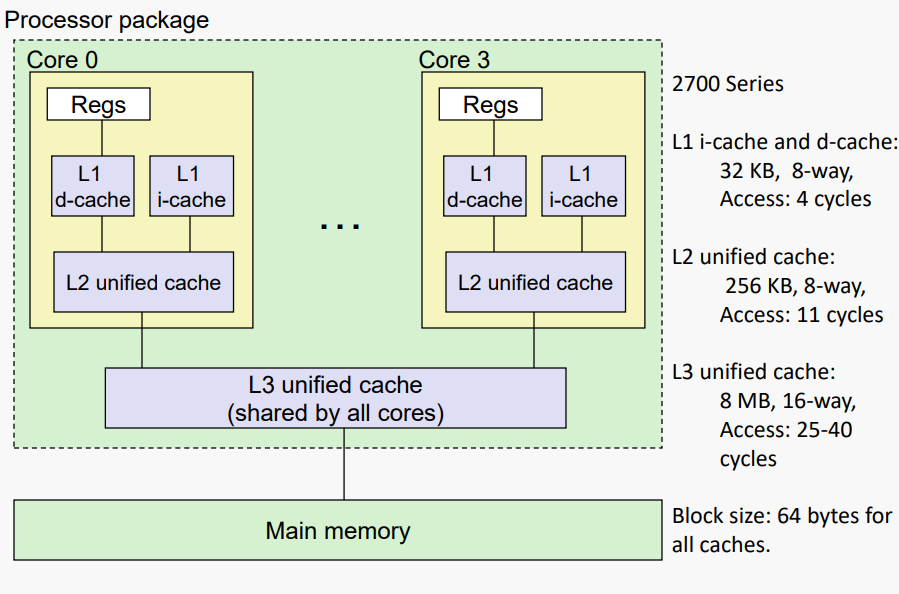
'Computer Science > Computer Organization' 카테고리의 다른 글
| [Lecture 19] Virtual Memory: Hardware and Performance (1) | 2022.11.12 |
|---|---|
| [Lecture 15] Memory Hierarchy / Cache Memory and Performance (1) | 2022.11.11 |
| [Lecture 14] Pipeline Handling Branches (0) | 2022.11.10 |
| [Lecture 8] Computer Performance (0) | 2022.11.09 |



