#Binary Trees
Binary Tree, 이진트리란 컴퓨터 과학에서 사용되는 데이터 구조의 하나로, 뿌리가 있는 나무 구조(트리, tree)에서 어떤 노드의 자식의 수가 최대 2개를 넘지 않는 트리를 말한다. 이진 트리는 비어 있거나 루트의 왼쪽 하위 트리와 오른쪽 하위 트리라고 불리는 두 개의 이진 트리와 함께 루트라고 불리는 노드로 구성되어 있다
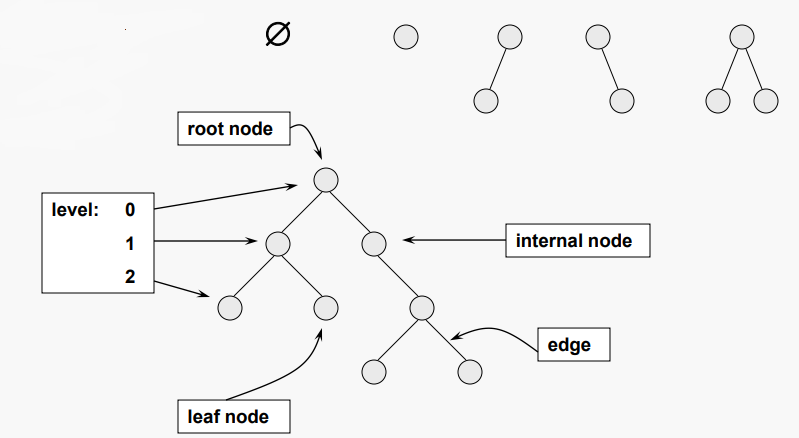
한 노드의 자식 노드가 최대 2개(왼쪽, 오른쪽)인 자료구조로, 이진 탐색 트리(binary search tree) 및 힙(heap) 등을 구현하기 위해 사용된다. 이진 트리에서의 방향 간선, 루트 노드, 단말 노드, 각 노드의 깊이, 레벨, 트리의 높이, 노드의 차수 등에 대한 정의는 일반적인 트리에 대한 용어 정의와 동일하다. 하지만 이진 트리는 뿌리 노드를 중심으로 2개의 부-트리(sub tree)로 나뉘어지며, 나뉘어진 2개의 부-트리도 모두 이진 트리여야 한다는 조건을 만족해야 한다. 이진 트리의 구조는 다음과 같다.

이진 트리의 종류로는 포화 이진 트리(Full Binary Tree), 완전 이진 트리(Complete Binary Tree), 높이 균형 트리(Height Balanced Tree), 완전 높이 균형 트리(Completely Height Balanced Tree) 등이 있으며, 각각의 특징은 다음과 같다.
- 포화 이진 트리 : 모든 레벨의 노드가 꽉 차있으며, 단말 노드를 제외한 모든 노드의 차수가 2인 이진 트리.
- 완전 이진 트리 : 단말 노드들이 트리 왼쪽부터 채워진 형태의 이진 트리.
- 높이 균형 트리 : 모든 단말 노드의 깊이 차이가 많아야 1인 이진 트리.
- 완전 높이 균형 이진 트리 : 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 이진 트리.
[Naver: binary tree]
#Binary Tree 노드 관계
이진 트리 노드에는 0, 1 또는 2개의 하위 노드가 있을 수 있다.
경로는 트리에 있는 인접 노드의 시퀀스이다.
이진 트리의 하위 트리가 비어 있거나 해당 트리의 노드와 모든 하위 노드로 구성되어 있다

#Expression Trees
이진 트리는 대수적 표현을 표현하기 위해 사용될 수 있다. 각 하위 트리는 전체 식의 일부를 나타낸다. 이진 트리의 노드를 올바른 순서로 방문하면 대수식을 구성할 수 있다

#Traversals
트래버설(traversal)은 이진 트리의 노드 일부 또는 전체를 일정한 순서로 방문하는 알고리즘이다.
이진 트리의 모든 노드를 방문하는 트래버설을 enumeration이라고 한다.

다음과 같은 이진트리가 있다고 가정하자
preorder: 노드를 방문한 다음 왼쪽 하위 트리, 오른쪽 하위 트리를 차례로 방문

postorder: 왼쪽 하위 트리, 오른쪽 하위 트리, 노드를 차례로 방문

inorder: 왼쪽 하위 트리, 노드, 오른쪽 하위 트리를 방문

#Postorder Traversal Details
재귀적 관점에서 포스트 오더 트래버설을 보자
왼쪽 하위 트리를 방문.
오른쪽 하위 트리를 방문.
그런 다음 노드를 방문한다(재귀 없음)
루트에서 트래버설 시작시:

#Binary Search Trees
일반적인 이진 트리는 실제로 매우 유용하지 않다. 이진 트리의 주요 용도는 데이터에 대한 빠른 액세스(인덱싱)를 제공하는 것이며 일반 이진 트리는 성능이 좋지 않다.
여러 필드를 포함하는 데이터 요소를 저장하려고 하고 이러한 필드 중 하나가 검색을 수행할 키로 구분된다고 가정하자.
이진 검색 트리 또는 BST는 비어 있거나 각 노드의 데이터 요소에 키가 있는 이진 트리이다. 이진탐색트리는 이진트리 구조에서 출발한다. 데이터의 값에 따라 자리가 정해져, 자료의 탐색, 삽입, 삭제가 효율적인 구조를 말한다.
여기서 이진트리란 최상위 루트 노드(트리 구조에서 데이터가 들어가는 한 칸)로부터 하위 트리로 갈 때 가질 수 있는 자식의 노드수가 2개 이하인 트리구조를 말한다. 즉 왼쪽, 오른쪽 아래쪽으로 자식 노드를 가질 수 있는 구조다.
이진탐색트리는 이 이진트리에 3가지 조건을 더 갖는 트리구조를 말하며 그 조건은 다음과 같다.
1. 왼쪽 하위 트리의 모든 키(있는 경우)가 루트 노드의 키보다 작다.
2. 오른쪽 하위 트리의 모든 키(있는 경우)는 루트 노드의 키보다 크거나 같다.
3. 루트의 왼쪽과 오른쪽 하위 트리는 이진 검색 트리이다.
예를 들어, 이진탐색트리에서 특정 값을 찾는 연산은
1. 검색을 원하는 데이터값 = 루트 노드 : 원하는 원소 찾았으므로 탐색 성공
2. 검색을 원하는 데이터값 〈 루트 노드 : 루트 노드의 왼쪽 서브 트리에서 탐색
3. 검색을 원하는 데이터값 〉 루트 노드 : 루트 노드의 오른쪽 서브 트리에서 탐색
#BST Insertion
여기서 키 값은 문자이다(키 값만 표시됨). 다음 키 값을 지정된 순서대로 삽입하면 지정된 BST가 생성된다. BST에서 삽입은 항상 리프 레벨에 있다. 적절한 지점을 찾을 때까지 BST를 통과하여 새 값을 기존 값과 비교한 다음 해당 값을 보유하는 새 리프 노드를 추가한다
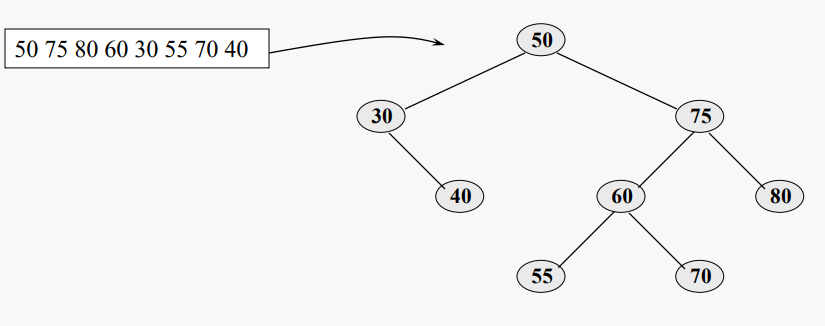
결과값: 30 40 50 55 60 70 75 80
#BST 탐색
BST에 의해 부과된 키 순서 때문에 검색은 정렬된 배열의 이진 검색 알고리즘과 유사하며, 이는 N개의 요소의 배열에 대한 O(log N)이다. BST는 순수하게 동적인 스토리지의 이점을 제공하며, 어레이 셀을 낭비하지 않으며 삽입 및 삭제 시 어레이 테일을 이동하지 않는다
그렇다면, 아래와 같이 이진트리에서 12를 검색하고자 할 때에는 어떻게 진행 될까?
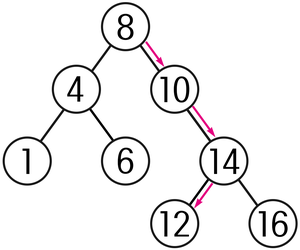
1. 루트 노드 값인 8과 찾고자 하는 수 12를 비교했을 때 검색을 원하는 데이터 값(12)이 크므로 루트 노드의 오른쪽 서브 트리에서 탐색을 한다.
2. 그 다음 루트인 10과 비교를 해서 12가 크므로 또 10의 오른쪽 서브 트리에서 탐색을 한다.
3. 그 다음 루트인 14와 비교를 해서 12가 작으므로 14의 왼쪽 서브 트리에서 탐색을 한다.
4. 12 검색
이처럼 이진 트리 구조는 데이터 값에 따라 왼쪽 자식노드가 루트보다 값이 작고, 오른쪽 자식 노드가 루트보다 값이 크도록 정해져 있다. 데이터 값이 크기에 따라 정리가 된다는 점 때문에 데이터를 검색, 삽입, 삭제하기에 편리한 구조이다
[Naver]
#BST 삭제
- 알고리즘이 BST를 생성해야 하기 때문에 BST에서 삭제는 아마도 가장 복잡한 작업일 것이다. 문제는 삭제된 값을 대체해야 하는 값이다. 일반 트리와 마찬가지로 다음과 같은 경우가 있다
- 리프 노드를 제거하는 것은 어렵지 않은 작업이다. 상위 노드의 관련 하위 포인터를 NULL로 설정한다
- 하위 트리가 하나만 있는 내부 노드를 제거하는 것도 사소한 일이지만 상위 노드에서 하위 트리의 루트를 대상으로 관련 하위 포인터를 설정하기만 하면 된다
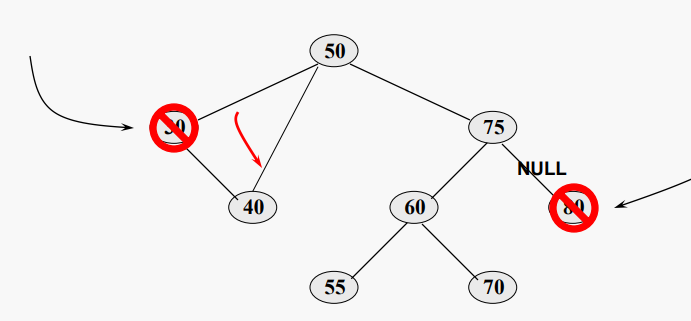
하지만 두 개의 하위 트리가 있는 내부 노드를 제거하는 것은 더 복잡하다
노드를 제거하기만 하면 트리의 연결이 끊어진다. 그렇다면 대상 노드의 값을 대체해야 하는 값은 무엇일까? BST 속성을 보존하려면 오른쪽 하위 트리에서 가장 작은 값을 가져와야 한다. 이 값은 삭제되는 값의 가장 가까운 계승자이다.
또는
왼쪽 하위 트리에서 가장 큰 값으로, 삭제되는 값의 가장 가까운 이전 값이다
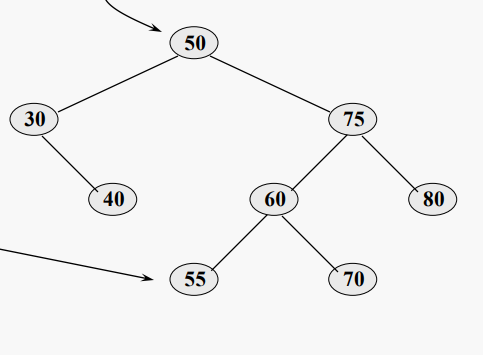
먼저 오른쪽 하위 트리의 가장 왼쪽 노드를 찾은 다음 해당 노드와 대상 노드 간에 데이터 값을 교환한다.
이 시점에서 반드시 BST가 있는 것은 아니다
이제 오른쪽 하위 트리에서 복사된 값을 삭제해야 한다
문제의 노드가 리프이기 때문에 여기서 그것은 간단해 보인다. 하지만
- 노드가 모든 경우에 리프가 되지는 않는다.
- 중복된 값의 발생은 복잡한 요인이다.
- 그래서 우리는 이 시점에서 정리하기 위해 DeleteRightMinimum() 기능을 쓰고 싶을 수 있다
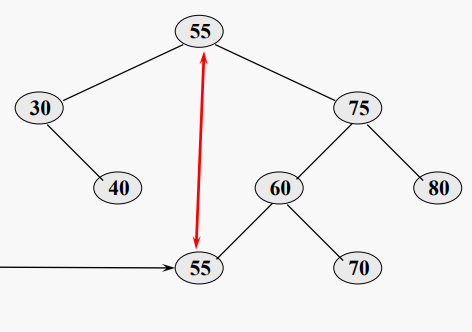
BST에서 값 55를 삭제한다고 가정하자. 55를 60으로 교체한 후, 삭제해야 한다. 또한 값 75를 삭제하는 것도 고려해 보십시오. 이 경우 오른쪽 하위 트리는 원래 삭제 대상 노드인 리프 노드일 뿐이다
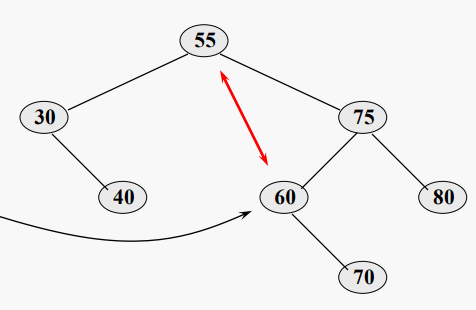
#BST에서의 밸런스
노드가 N개인 BST는 항상 O(log N) 검색 시간을 제공하지는 않는다.
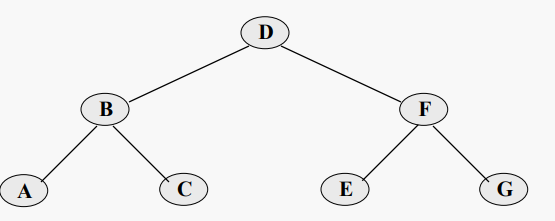
균형 잡힌 BST. 최악의 경우 로그(N) 검색 시간이다
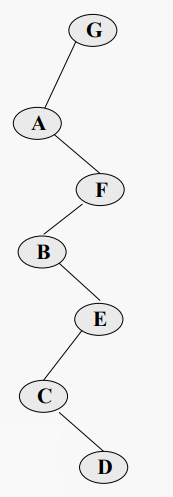
균형이 맞지 않는 BST. 최악의 검색 시간도, 평균 검색 시간도 로그(N)이 아니다
#Search Cost in a BST
우리는 이제 L 노드를 포함하는 이진 트리는 최소 1 + log L 수준을 포함해야 한다는 것을 알고 있다.
트리가 가득 찬 경우 N개의 노드를 포함하는 전체 이진 트리에 적어도 N개의 로그 수준이 포함되어야 함을 암시하도록 결과를 개선할 수 있다.
따라서 모든 BST에 대해 검색 비용이 적어도 log N인 요소가 항상 존재힌다.
하지만 탐색시간은 훨씬 더 나쁠 수 있다. 만약 BST가 "stalk"라면, 마지막 요소의 검색 비용은 N이 될 것이다.
이 모든 것은 한 가지 간단한 문제로 나타나진다: 트리가 최소 높이에 얼마나 가깝나?
BST에서 많은 무작위 삽입과 삭제를 수행한다면, 결과가 거의 최소 높이를 가질 가정할 수 없다.
트리의 모든 레벨이 완전히 가득 차도록 이진 트리가 있다고 가정하자. 예시:
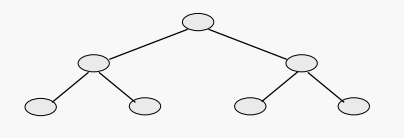
분명히, 우리는 주어진 이진 트리를 이 속성을 갖도록 "확장"할 수 있고, 이와 같은 트리는 우리가 트래버설에 대한 최악의 경우에 대한 경계를 얻을 수 있게 해준다.
세 개의 표준 순회는 각각 트리의 모든 노드로 이동하며, 순회 비용은 실제로 현재 노드가 처리되는 순서에 영향을 받지 않는다.
노드로 수행하는 모든 작업의 비용이 1이라고 가정해 보자.
그리고, W(N)가 N개의 노드를 가진 이진 트리를 통과하는 비용을 나타내도록 하자.
트래버설 과정에서 어느 노드에있던간에 우리는 다음 3가지를 수행해야한다
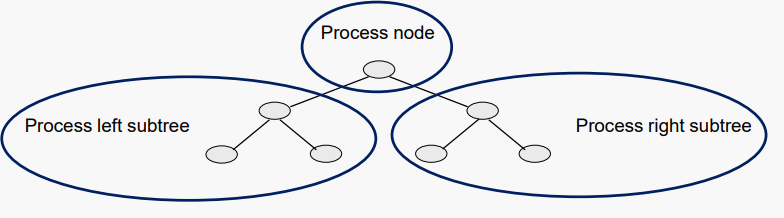
따라서, 우리는 순회 비용에 대한 재귀적 정의를 다음과 같이 쓸 수 있다
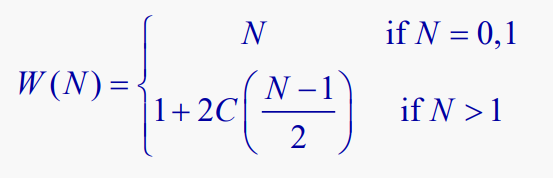
#BST에서 삽입/삭제 비용
일단 상위 노드가 발견되면, BST에 새 노드를 삽입하는 데 드는 남은 비용은 일정하며, 단순히 새로운 노드 개체를 할당하고 상위 노드에 포인터를 설정하는 것이다.
따라서 삽입 비용은 기본적으로 검색 비용과 동일하다.
삭제의 경우 인수가 약간 더 복잡하다. 대상 노드의 상위 노드가 발견되었다고 가정하자.
상위 항목에 하위 트리가 하나만 있는 경우, 나머지 비용은 상위 항목의 포인터를 재설정하고 노드를 할당 해제하는 것이다. 이는 일정하다.
그러나 상위 하위 트리가 두 개인 경우 오른쪽 하위 트리에서 최소 값을 찾기 위해 추가 검색을 수행해야 하며, 요소 복사를 수행한 다음 해당 노드를 오른쪽 하위 트리에서 제거해야 한다(이는 일정한 비용임).
어떤 경우든, 우리는 잎 수준까지 최악의 경우 검색 비용과 몇 가지 지속적인 조작 이상의 것이 없다.
따라서 삭제 비용도 기본적으로 검색 비용과 동일하다.
#BST 구현
이제 BST를 Java를 사용하여 구현해보자. 여기 BST interface가 있다
public class BST<T extends Comparable<? super T>> {
class BinaryNode {
. . .
T element; // the data in the node
BinaryNode left; // pointer to the left child
BinaryNode right; // pointer to the right child
}
BinaryNode root; // pointer to root node, if present
public BST( ) { . . . }
public boolean isEmpty( ) { . . . }
public T find( T x ) { . . . }
public boolean insert( T x ) { . . . }
public boolean remove( T x ) { . . . }
public void clear( ) { . . . }
public boolean equals(Object other) { . . . }
// private methods follow
}#Generic Type Bounds
public class BST<T extends Comparable<? super T>> {
. . .
}
//public int compareTo(Object o)이 개체가 지정된 개체보다 작거나 같거나 크므로 음의 정수, 0 또는 양의 정수를 반환한다.
왜 Type Bound가 필요할까?
BST는 삽입된 데이터 개체에 대해 세 값의 비교를 수행할 수 있어야 한다.
자바 클래스는 그러한 능력을 제공한다는 보장이 없다.
이것은 삽입된 개체가 지원하는 능력에 대한 "하한"을 지정한다.
그 능력들은 슈퍼 클래스로부터 물려받을 수 있다
#Generic BST 노드
class BinaryNode {
// Constructors
public BinaryNode( T elem) {
. . .
}
public BinaryNode( T elem, BinaryNode lt, BinaryNode rt ) {
. . .
}
// The node class and the following members have package access:
T element; // The data in the node
BinaryNode left; // Pointer to the left child
BinaryNode right; // Pointer to the right child
}#BST find() 구현
BST find() 함수는 트리 내의 데이터 개체에 대한 클라이언트 액세스를 제공한다
public T find( T x ) {
return find( x, root );
}private T find( T x, BinaryNode sRoot ) {
if ( sRoot == null )
return null;
int compareResult = x.compareTo( sRoot.element );
if ( compareResult < 0 )
return find( x, sRoot.left );
else if ( compareResult > 0 )
return find( x, sRoot.right );
else
return sRoot.element; // Match
}#BST insert() 구현
public insert() 함수는 재귀 helper를 호출하기 위한 stub일 뿐이다
public boolean insert( T x ) {
root = insert( x, root );
. . .
}stub은 단순히 helper function을 호출한다.
helper function은 트리에서 새 노드를 배치할 적절한 위치를 찾아야 한다.
설계 논리는 간단하다: 새 잎의 부모 "노드"를 찾아 새 잎을 오른쪽에 매달아 놓는다
#BST insert() Helper
private BinaryNode insert( T x, BinaryNode sRoot ) {
if ( sRoot == null )
return new BinaryNode( x, null, null );
int compareResult = x.compareTo( sRoot.element );
if ( compareResult < 0 )
sRoot.left = insert( x, sRoot.left );
else if ( compareResult > 0 )
sRoot.right = insert( x, sRoot.right );
else
; // Duplicate; do nothing
return sRoot;
}새 값의 상위를 찾으면 한 번 더 재귀 호출이 발생하여 도우미 함수에 null 포인터를 전달한다.
삽입 도우미 함수는 노드 포인터 매개 변수를 수정할 수 있어야 하며 검색 로직은 find() 함수와 정확하게 동일하다
#BST insert() Helper 로직
private BinaryNode insert( T x, BinaryNode sRoot ) {
if ( sRoot == null )
return new BinaryNode( x, null, null );
int compareResult = x.compareTo( sRoot.element );
if ( compareResult < 0 )
sRoot.left = insert( x, sRoot.left );
. . .
return sRoot;
}새 노드를 설치할 때 상위 노드에서 참조를 수정해야 한다.
자바 참조는 원시적이며 우리는 원시적인 참조를 전달할 수 없다
여기서 설계는 "falls off a branch of the tree" 호출 중에 새 노드를 생성하고 상위 노드의 호출로 돌아간 후 새 노드를 설치한다
#BST delete() 구현
delete() 함수는 insert()와 비슷하다.
public boolean delete( T x ) {
root = delete( x, root );
. . .
}- delete() helper function 설계도 비교적 간단하다
- 목표값을 포함하는 노드의 상위 위치를 찾는다
- (앞에서 설명한 대로) 삭제 사례를 결정하고 처리
- 부모는 하나의 하위 트리만 가지고 있다
- 부모가 두개의 하위 트리를 가지고 있다
- 삭제 helper function 구현에 대한 자세한 내용은 작성자에게 달려 있다
#Parent Pointers
일부 이진 트리 구현은 노드에 상위 포인터를 사용한다
- 트리의 메모리 비용을 증가시킨다(거의 없음).
- 논리 삽입/삭제/복사의 복잡성 증가(매우)
- 삽입/삭제를 구현할 때 몇 가지 불필요한 대안을 제공한다.
- 실제로 트리에 반복자 추가를 단순화할 수 있다.
주어진 BST 템플릿은 다음과 같은 추가 기능을 제공할 수 있다
트리의 크기를 제공하는 함수
트리의 수준 수를 제공하는 함수
유용한 방법으로 트리를 표시하는 함수
또한 테스트 중에 계측기를 사용하는 것도 유용하다. 예를들면
검색 중에 발견된 값과 검색한 방향을 기록
이것은 또한 추가하기 쉽지만, 우리는 일반적으로 BST를 사용할 때 그러한 출력을 보고 싶지 않기 때문에 문제를 제기한다.
클라이언트가 출력 스트림을 개체와 선택적으로 연결하고 필요에 따라 작업 로깅을 설정하거나 해제할 수 있도록 템플릿에 몇 가지 데이터 멤버와 변환기를 추가하여 이 문제를 해결한다.
#Full and Complete Binary Trees
여기 두 가지 중요한 이진 트리가 있다. 정의는 비슷하지만 논리적으로 독립적이다
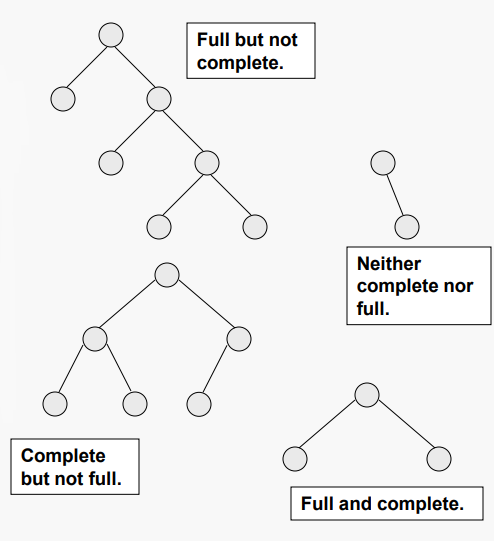
이진 트리 T는 각 노드가 리프이거나 정확히 두 개의 자식 노드를 가진 경우 full이다.
n개의 레벨을 가진 이진 트리 T는 마지막 레벨을 제외한 모든 레벨이 완전히 채워지고 마지막 레벨은 모든 노드가 왼쪽에 있는 경우 complete이다.
#Full Binary Tree Theorem
정리: T를 비어 있지 않은 전체 이진 트리로 지정하면 다음과 같다.
(a) 만약 T가 I개의 내부 노드를 가지고 있다면, 잎의 수는 L = I + 1이다.
(b) T에 I개의 내부 노드가 있는 경우 총 노드 수는 N = 2I + 1이다.
(c) 만약 T가 총 N개의 노드를 가지고 있다면, 내부 노드의 수는 I = (N – 1)/2이다.
(d) 만약 T가 총 N개의 노드를 가지고 있다면, 잎의 수는 L = (N + 1)/2이다.
(e) 만약 T가 L개의 잎을 가지고 있다면, 총 노드 수는 N = 2L – 1이다.
(f) 만약 T가 L개의 잎을 가지고 있다면, 내부 노드의 수는 I = L – 1이다.
기본적으로, 이 정리는 노드 N의 수, L의 수, 그리고 내부 노드 I의 수가 서로 관련이 있다는 것을 말하며, 만약 여러분이 그들 중 하나를 알고 있다면, 나머지 두 개를 결정할 수 있다
#Full Binary Tree 증명
(a)의 증명: 우리는 내부 노드의 수, I에 대한 유도를 사용할 것이다. 만약 T가 I 내부 노드를 가진 완전한 이진 트리라면, T는 I + 1 리프 노드를 가질 수 있도록 모든 정수 I ≥ 0의 집합이라고 하자.
기본 케이스의 경우 I = 0이면 트리가 루트 노드로만 구성되어야 하며 트리가 가득 차서 하위 노드가 없어야 한다. 따라서 1개의 리프 노드가 있고, 따라서 0 ∈ S이다.
이제 어떤 정수 K ≥ 0일 때, 0에서 K까지의 모든 I가 S에 있다고 가정하자. 즉, T가 I 내부 노드를 갖는 비어 있지 않은 완전 이진 트리이며, 여기서 0 ≤ I ≤ K이고, T는 I + 1 리프 노드를 갖는다.
T를 K + 1개의 내부 노드를 가진 완전 이진 트리라고 하자. 그러면 T의 루트는 두 개의 하위 트리 L과 R을 가지고 있다; L과 R이 각각 IL과 IR 내부 노드를 가지고 있다고 가정하자. L과 R은 둘 다 비워둘 수 없으며, L과 R의 모든 내부 노드는 T의 내부 노드여야 하며, T는 하나의 추가 내부 노드(루트)를 가지고 있으므로 K + 1=IL + IR + 1이다.
이제 귀납 가설에 따르면, L은 IL+1 잎을 가지고 R은 IR+1 잎을 가져야 한다. T의 모든 잎은 L 또는 R의 잎이어야 하므로, T는 IL + IR + 2개의 잎을 가져야 한다.
따라서, 적은 양의 대수학을 할 때, T는 K + 2개의 리프 노드를 가져야 하고, 따라서 K + 1 ∈ S를 가져야 한다. 따라서 수학적 귀납법에 의해, S = [0, ∞).
#리프 수 Limit
Theorem: T를 level이 λ개인 이진 트리로 하자. 그렇다면 잎의 수는 최대 2^(λ-1)이다
증명: 우리는 레벨 수 λ에 대해 강한 유도를 사용할 것이다. 만약 T가 레벨이 l인 이진 트리라면 T는 최대 2(λ-1)개의 리프 노드를 가질 수 있도록 모든 정수 λ ≥ 1의 집합이라고 하자.
기본 케이스의 경우 σ = 1이면 트리에 하나의 노드(루트)가 있어야 하며 하위 노드가 없어야 한다. 따라서 1개의 리프 노드(λ = 1일때 2λ-1)가 있고, 따라서 1∈S가 있다.
이제 어떤 정수 K ≥ 1일 때, 모든 정수 1에서 K까지의 모든 정수가 S라고 가정하자. 즉, 이진 트리가 M ≤ K인 레벨을 가질 때마다 최대 2M-1 리프 노드를 갖는다.
T를 K + 1 수준의 이진 트리로 하자. 만약 T가 최대 리프 수를 가지고 있다면, T는 루트 노드와 두 개의 비어 있지 않은 서브 트리, 예를 들어 S1과 S2로 구성된다. S1과 S2에 각각 M1과 M2 수준이 있다고 하자. M1과 M2는 1과 K 사이에 있기 때문에, 귀납적 가정에 의해 각각은 S에 있다. 따라서, S1 및 S2의 리프 노드의 수는 각각 최대 2K-1 및 2K-1이다. T의 모든 잎은 S1 또는 S2의 잎이어야 하기 때문에, T의 잎의 수는 최대 2K-1 + 2K-1이다. 따라서, K +1은 S에 있다.
따라서 수학적 귀납법에 의해, S = [1, ∞].
그 외의 Theorem들
Theorem: T를 이진 트리로 하자. k ≥ 0일 때마다 레벨 k에는 2^k개 이하의 노드가 있다.
Theorem: T를 λ level의 이진 트리로 하자. 그러면 T는 2^(λ – 1)개의 노드를 가질 수 있다.
Theorem: T를 N개의 노드를 가진 이진 트리라고 하자. 그럼 트리의 level의 수는 적어도 ⌈log (N + 1)⌉개이다
Theorem: T를 L개의 잎을 가진 비어 있지 않은 이진 트리라고 하자. 그럼 트리의 level의 수는 적어도 ⌈log L⌉ + 1개이다
'Computer Science > Data Structures & Algorithms' 카테고리의 다른 글
| [Lecture 7] 점근(asymptotic) 표기법/ Big-O 표기법 (1) | 2023.01.06 |
|---|---|
| [Lecture 6] Algorithm Analysis / 알고리즘 분석 (1) | 2023.01.05 |
| [Lecture 4] Hash Function / 해시 함수 (1) | 2023.01.03 |
| [Lecture 0 - II] Java Equals() & Generics (0) | 2023.01.01 |
| [Lecture 0 - I] Java File I/O (1) | 2023.01.01 |



