#알고리즘
알고리즘(algorithm)은 특정 문제 또는 문제의 모음을 해결하기 위해 수행할 일련의 작업을 지정하는 유한한 명령 집합이다. 간단히 말해 주어진 문제를 논리적으로 해결하기 위해 필요한 절차, 방법, 명령어들을 모아놓은 것이다. 넓게는 사람 손으로 해결하는 것, 컴퓨터로 해결하는 것, 수학적인 것, 비수학적인 것을 모두 포함한다.
- 알고리즘은 다음과 같은 속성을 가져야 한다:
- 유한성 / finiteness: 알고리즘은 한정된 수의 명령이 실행된 후에 완료되어야 한다.
- 명료성 / unambiguity: 각 단계는 하나의 해석만 가지고 명확하게 정의되어야 한다
- 수열의 정의 / definition of sequence: 각 단계에는 고유하게 정의된 선행과 후속 단계가 있어야 한다. 첫 번째 단계(시작 단계)와 마지막 단계(정지 단계)를 명확히 기록해야 한다.
- input/output: 필요한 input과 output의 수와 타입을 지정해야 한다
- 실현 가능성 / feasibility: 각 명령이 실현 가능해야 한다
#알고리즘 VS 프로그램
프로그램이란 컴퓨터를 실행시키기 위해 차례대로 작성된 명령어 모음이다. 그렇기 때문에 특정 프로그래밍 언어로 된 알고리즘의 구체적인 표현 이라고 설명된다.
해결해야 할 문제가 주어지면, 설계 단계는 알고리즘을 생성한다. 그런 다음 구현 단계는 설계된 알고리즘을 표현하는 프로그램을 생성한다

특정한 문제가 주어지면, 일반적으로 그 문제를 해결할 많은 다른 알고리즘들이 있다. 디자이너는 그 알고리즘들 중에서 합리적인 선택을 해야 한다
- 알고리즘 설계 고려 사항
- 이해, 구현 및 디버깅이 쉬운 알고리즘을 설계해야 한다(소프트웨어 엔지니어링)
- 이용 가능한 계산 자원(데이터 구조 및 알고리즘 분석)을 효율적으로 사용하는 알고리즘을 설계해야 한다
그렇다면 알고리즘의 효율성을 어떻게 측정할까? 수행할 작업의 수와 필요한 공간은 처리해야 하는 입력 값의 수에 따라 달라진다
#벤치마킹
다양한 크기의 입력 데이터에서 프로그램을 실행하고 실행을 위한 시간을 측정함으로써 구현을 생성한 다음 벤치마킹 분석을 수행함으로써 알고리즘의 효율성을 측정하는 것이 좋다.
- 하지만:
- 프로그램은 알고리즘의 가능성을 제대로 표현하지 못할 수 있다.
- 결과는 아마도 미묘한 방식으로 벤치마킹에 사용되는 하드웨어의 특정 특성에 따라 달라질 것이다.
- 테스트 데이터의 선택은 알고리즘의 동작에 영향을 미치는 다양한 요인의 대표적인 샘플링을 제공하지 않을 수 있다
#Complexity Analysis / 복잡성 분석
복잡도 분석은 계산 비용에 대한 체계적인 연구이며, 수행된 시간 단위 또는 작업 또는 필요한 저장 공간의 양으로 측정된다
목표는 운영 플랫폼과 독립적으로 알고리즘 및/또는 구현을 비교할 수 있는 의미 있는 척도를 갖는 것이다
- 복잡성 분석에는 두 가지 다른 단계가 포함된다
- 알고리즘 분석: 복잡도를 측정하는 함수 T(n)를 생성하기 위한 알고리즘 또는 데이터 구조의 분석
- 크기 순서(점근적) 분석: 함수 T(n)를 분석하여 함수가 속한 일반적인 복잡도 범주를 결정한다.
#Algorithm Analysis / 알고리즘 분석
알고리즘 분석(영어: analysis of algorithms)은 컴퓨터 과학에서 알고리즘을 실행하는데 필요한 (시간과 기억 용량과 같은) 자원의 수를 결정하는 일을 가리킨다. 대부분의 알고리즘은 임의의 길이의 입력과 함께 동작하도록 구성된다. 일반적으로 알고리즘의 효율성과 실행 시간은 단계의 수 (시간 복잡도)와 기억 위치 (공간 복잡도)에 대한 입력 길이와 관련한 함수로 나타낼 수 있다. 쉽게 말해 알고리즘의 성능을 평가하기 위한 분석. 이 성능은 크게 그 수행 시간과 필요한 기억 장치의 양으로 평가되는데, 많은 경우에 수행 시간이 더 중요한 의미를 지닌다.
알고리즘 분석이 더 광범위한 계산 복잡도 이론의 중요한 부분인데, 주어진 계산 문제를 해결하는 알고리즘에 필요한 자원에 대한 이론적 견적을 제공한다. 이러한 견적들은 효율적인 알고리즘을 검색하는데 도움을 준다.
알고리즘의 분석 목적은 알고리즘 수행 시간을 예측하고 확인함으로써 더욱 효율적인 알고리즘을 개발하기 위한 것이다. 하나의 명령문을 수행하는 실제 시간은 컴퓨터 기종과 컴파일러에 의해 차이가 있으므로 계산 시간에 의한 분석은 명령문의 수행 빈도 수를 기준으로 한다. 이것은 사용하는 프로그래밍 언어나 컴파일러 기종에 관계없이 알고리즘으로부터 직접 구할 수 있다.
알고리즘 분석에서는 보통 점근적(asymptotic) 의미로 복잡도를 계산한다. 즉, O표기법, Ω표기법, Θ표기법과 같은 방법으로 일정 크기의 입력 자료에 대한 복잡도 함수를 구한다. 예를 들어, 이진 탐색의 단계 수는 입력 자료의 크기에 대수적으로 비례하는데, 이것을 O(log n) 또는 대수 시간이라 한다. 점근적인 방법을 사용하는 이유는, 같은 알고리즘이라도 입력 자료의 크기에 따라 수행 시간에 차이가 나는 것을 보완하기 위해서이다. 이런 수행 시간의 차이는 상수 배로 나타나는데, 이때의 상수를 숨은 상수(hidden constant)라고 한다.
[네이버 지식백과 / wikipedia]
알고리즘 분석에는 연산을 계산하는 방법을 결정하는 일련의 규칙이 필요하다. 알고리즘 분석을 위해 일반적으로 허용되는 규칙 집합은 없다. 어떤 경우에는 정확한 연산 개수가 필요하지만, 다른 경우에는 일반 근사치로 충분하다. 다음에 제시된 규칙은 정확한 작동 횟수를 산출하기 위한 규칙의 전형이다.
#Exact Analysis 규칙
- 임의의 시간 단위를 가정한다
- 다음 작업 중 하나를 실행하는 데는 시간 1이 걸린다고 해보자
- a) 할당 작업
- b) 단일 I/O 작업
- c) 단일 부울 연산, 숫자 비교
- d) 단일 산술 연산
- e) 함수 반환
- f) 배열 인덱스 작업, 포인터 참조
- 선택 문(if, switch)의 실행 시간은 (조건 평가 시간 / condition evaluation)+ (선택의 individual clauses에 대한 실행 시간의 최대값) 이다.
- 루프 실행 시간은 루프가 실행된 횟수에 걸쳐 루프 검사 및 업데이트 작업에 대한 본문 시간 + 루프 설정에 대한 시간의 합이다. 루프가 가능한 최대 반복 횟수를 실행한다고 항상 가정한다
- 함수 호출의 실행 시간은 설정에 대해 1 + 매개 변수 계산에 대한 시간 + 함수 본문의 실행에 필요한 시간이다
#분석 예제1

따라서, n개의 입력값이 input되었다고 가정하면, 총 시간 T(n)은 다음과 같이 주어진다

#분석 예제2

따라서, T(n)의 총 시간은 다음과 같다

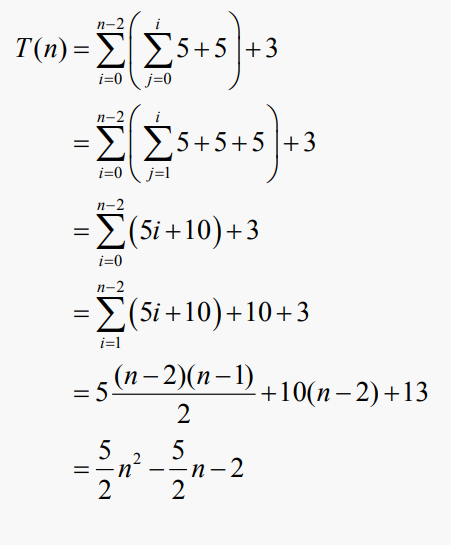
#분석 예제3

까다로운 부분은 외부 루프가 약 log(n)번 실행된다는 것이다. 정확하게, n은 2^log(n)와 같기 때문에, p가 현재 패스의 수(1부터 시작하는 숫자)라면 다음과 같이 주장할 수 있다:
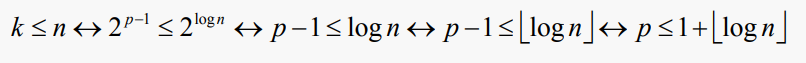
따라서, 이전 알고리즘에 대한 총 시간 T(n)은 다음과 같이 주어진다
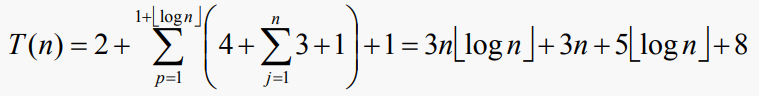
만약 우리가 n이 2의 거듭제곱이라고 가정한다면, floor 표기법은 사용하지 않아도 된다. 복잡도 함수를 표현할 때 차이가 작기 때문에 그렇게 하는 것이 일반적이다.
#분석 예제4
이제 간단한 선형 검색 함수를 한번 보자
int linearSearch(int List[], int Target, int Sz) {
for (int i = 0; i < Sz; i++) { // 1 before, 2 each pass, 1 exit
if ( Target == List[i] ) // 2
return i; // 1, if done
}
return Sz; // 1, if done
}List에서 Target이 발생하지 않을 경우 최악의 경우 비용이 발생한다. 이 경우:

반대로 Target이 List의 인덱스 0에서 발생할 경우 최상의 비용이 발생한다. 이 경우:

그렇다면 평균적인 비용은 어떨까? 목록의 K 인덱스에서 대상이 발생할 경우 검색 비용은 다음과 같다:

target이 list에 있다고 가정한 average-case 비용은 다음과 같다

실제 average-case 비용은 target이 list에서 발생할 확률에 따라 달라진다. 분명히 taget이 list에 없을 때의 검색 비용은 이전에 발견된 최악의 경우 비용이 될 것이다. 그러나 실제 평균 비용은 최악의 경우 성능을 달성한 검색 수에 따라 달라진다.
참고로, 데이터 객체의 비교만 계산할 경우, taget이 list에 있다고 가정한 평균 사례 비용은 다음과 같다:

#분석 예제5
이제 간단한 이진 탐색 함수를 보자:
int binSearch(int List[], int Target, int Sz) {
unsigned int Mid,
Lo = 0, // 1
Hi = Sz – 1; // 2
while ( Lo <= Hi ) { // 1 per pass + 1 for exit, if done
Mid = (Lo + Hi) / 2; // 3
if ( List[Mid] == Target ) // 2
return Mid; // 1, if done
else if ( Target < List[Mid] ) // 2, if done
Hi = Mid – 1; // 2, if done
else
Lo = Mid + 1; // 2, if done
}
return Sz; // 1, if done
}루프를 통과하는 한 번의 최악의 경우 비용은 10으로 볼 수 있다. 하지만 최악의 경우 몇 번의 패스가 필요할까? 다음과 같은 형태의 루프 조건을 보자: Hi – Lo > = 0
루프를 통과할 때마다(최악의 경우) Lo를 올리거나 Hi를 낮춘다. 어떤 것이 선택되든, 단순 수학은 연속적인 루프 테스트가 다음과 같다는 것을 보여준다:

분모는 2^p이다. 여기서 p는 수행하려는 패스의 수이다(p = 0으로 시작함). 상수 항은 2로 제한된다. 이제 Hi와 Lo의 초기화를 통해 Hi – Lo의 값은 Sz – 1에 불과하다. 따라서 문제는 기본적으로 다음 식을 언제 달성할 수 있느냐 하는 것이다:

위의 식은 우리가 다음과 같은 식이 필요하다는 것을 알려준다

그래서, 이진 탐색 함수의 T(N)은 다음과 같다

#복잡성이 중요한 이유?
우리가 알고리즘에서의 복잡성을 알아야 하는 이유가 무엇일까? 다음의 복잡도 함수의 차트를 한번 보자:

#실행 시간 추정
초당 106개의 명령을 실행할 수 있는 하드웨어가 있다고 가정하자. 복잡도 함수가 다음과 같은 알고리즘을 실행하는 데 걸리는 시간은 다음과 같다:

크기가 N = 10^8인 입력에서 수행되는 총 연산 수는 T(10^8)이다:

필요한 총 초의 수는 T(10^8)/10^6으로 주어지며, 따라서 다음과 같다:

sec/day 수는 86,400이므로 약 115,740일(317년)이 걸린다. 굉장히 느리다.
그렇다면 복잡도 함수가 다음과 같은 알고리즘을 사용하면 어떨까?

input size는 똑같이 N = 10^8이라고 가정해보자. 수행할 총 작업 수는 T(10^8)이다:

필요한 총 초의 수는 다음과 같이 T(10^8)/10^6으로 주어진다, 그렇기에:

위의 값을 분으로 환산해보면 44.33분 정도 된다. 317년보다 훨씬 빠른 속도이다
#Maximum Problem Size / 최대 문제 크기
이것을 보는 또 다른 방법은 알고리즘과 하드웨어 속도에 대한 복잡성 함수를 고려할 때 주어진 시간 내에 처리할 수 있는 가장 큰 문제 크기가 무엇인지 묻는 것이다. 이전과 동일한 하드웨어 속도를 가정할 때, T(N) = N^2 복잡성 함수가 다시 한번 반복된다면 1시간 내에 처리할 수 있는 최대 입력 크기는 얼마일까?

필요한 총 초의 수는 다시 T(N)/10^6으로 주어지므로 다음 중 N의 최대값이 무엇인지 묻고 있다:

위 식은 N ≤ 60,000을 산출한다
다음 복잡도 함수를 사용하여 동일한 논리를 적용해보자:
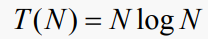
필요한 총 초의 수는 T(N)/10^6이므로 다음 중 N의 최대값이 무엇인지 묻고 있다:

Solving for equality (Newton's Method)를 사용하면 다음을 산출한다

여기서 우리가 첫 번째 알 수 있는 점은 큰 N의 경우 복잡성 함수가 중요하다는 것이다. 또한 큰 N의 경우 Nlog(N)이 N^2보다 훨씬 빠르다는 것이다.
두 번째 알 수 있는 점은 이 논리를 하드웨어 속도 향상 문제에 적용할 수 있다는 것이다
#더 빠른 하드웨어
동일한 분석을 적용하면 이전 하드웨어보다 100배 빠른 하드웨어를 찾을 수 있다고 가정할 때(초당 10^8회 작동) 결과는 다음과 같다

이전의 결과와 비교하여 하드웨어 속도를 100배 향상시키면 두 경우 모두 동일한 크기의 문제에 대한 시간이 100배 감소하므로 N log(N) 알고리즘의 상대적 이점이 유지된다. 또한 N log(N) 사례의 경우 거의 75의 인수에 비해 N^2 사례의 경우 최대 문제 크기를 10의 인수로 증가 시킨다.
'Computer Science > Data Structures & Algorithms' 카테고리의 다른 글
| [Lecture 13] B-Tree / B-트리 (0) | 2023.01.12 |
|---|---|
| [Lecture 7] 점근(asymptotic) 표기법/ Big-O 표기법 (1) | 2023.01.06 |
| [Lecture 4] Hash Function / 해시 함수 (1) | 2023.01.03 |
| [Lecture 1] BST / Binary Search Tree / 이진탐색트리 (0) | 2023.01.01 |
| [Lecture 0 - II] Java Equals() & Generics (0) | 2023.01.01 |



