#B-Tree Intro
전산학에서 B-트리(B-tree)는 데이터베이스와 파일 시스템에서 널리 사용되는 트리 자료구조의 일종으로, 이진 트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조이다. 쉽게 말해 다방향 탐색 트리이다. 대용량의 파일을 효율적으로 검색하고 갱신하기 위해 고안된 트리 형태의 자료 구조이다.
방대한 양의 저장된 자료를 검색해야 하는 경우 검색어와 자료를 일일이 비교하는 방식은 비효율적이다. B-트리는 자료를 정렬된 상태로 보관하고, 삽입 및 삭제를 대수 시간으로 할 수 있다. 대부분의 이진 트리는 항목이 삽입될 때 하향식으로 구성되는 데 반해, B-트리는 일반적으로 상향식으로 구성된다.
n개의 키 (s1,s2,s3...,sn)가 있는 한 노드를 생각해 보자. 키집합은 정렬되어 있다고 한다. (즉, s1<s2<s3...<sn) 그 노드는 n+1자식노드를 가리키는 포인터로 구성된다. 즉, t0,t1,t2...tn.
B-트리의 기본 개념은 내부 노드의 자식 노드의 수가 미리 정해진 범위 내에서 변경가능하다는 것이다. 항목이 삽입되거나 삭제될 때, 내부 노드는 해당 범위의 자식 노드의 수를 만족시키기 위해 분리되거나 혹은 다른 노드와 합쳐지게 된다. 자식 노드의 수가 일정 범위 내에서만 유지되면 되므로 분리 및 합침을 통한 재균형 과정은 다른 자가 균형 이진 탐색 트리만큼 자주 일어나지 않지만, 저장 공간에서의 손실은 있게 된다. 자식 노드의 최소 및 최대수는 일반적으로 특별한 구현에 대해서 결정되어 있다. 예를 들어, 2-3 B-트리(혹은 단순히 2-3 트리)에서 각 내부 노드는 2 또는 3개의 자식 노드를 가질 수 있다. 만약 허용되지 않은 수의 자식 노드를 가질 경우, 해당 내부 노드는 부적절한 상태에 있다고 한다.
B-트리는 노드 접근시간이 노드에서의 연산시간에 비해 훨씬 길 경우, 다른 구현 방식에 비해 상당한 이점을 가지고 있다. 이는 대부분의 노드가 하드디스크와 같은 2차 저장장치에 있을 때 일반적으로 일어난다. 각 내부 노드에 있는 자식 노드의 수를 최대화함으로써, 트리의 높이는 감소하며, 균형맞춤은 덜 일어나고, 효율은 증가하게 된다. 대개 이 값은 각 노드가 완전한 하나의 디스크 블록 혹은 2차 저장장치에서의 유사한 크기를 차지하도록 정해진다.
B-트리의 노드는 대개 항목과 자식 포인터의 순서 집합으로 표현된다. 루트 노드를 제외한 모든 노드는 임의의 수 L, U(L<U)에 대해 최소 L 항목, 최대 U 항목을 가지고 있으며, 최대 U+1개의 자식 포인터를 가지고 있다. 모든 내부 노드에서, 자식 포인터의 수는 언제나 항목 개수보다 하나가 많다. 모든 리프 노드가 동일한 높이에 있기 때문에, 노드는 일반적으로 리프 노드인지 내부 노드인지 판별하는 수단을 가질 이유가 없다.
각 내부 노드의 항목은 부트리를 나누는 구분 값이다. 예를 들어, 어떤 내부 노드가 3개의 자식 노드(혹은 부트리)를 가지고 있다면, 그 내부 노드는 두개의 구분 값이나 항목 a1과 a2를 가지고 있어야 한다. 가장 왼쪽 부트리에 있는 모든 값은 a1보다 작으며, 가운데 부트리의 모든 값은 a1와 a2의 사이에 있으며, 가장 오른쪽 부트리의 모든 값은 a2보다 크게 된다.
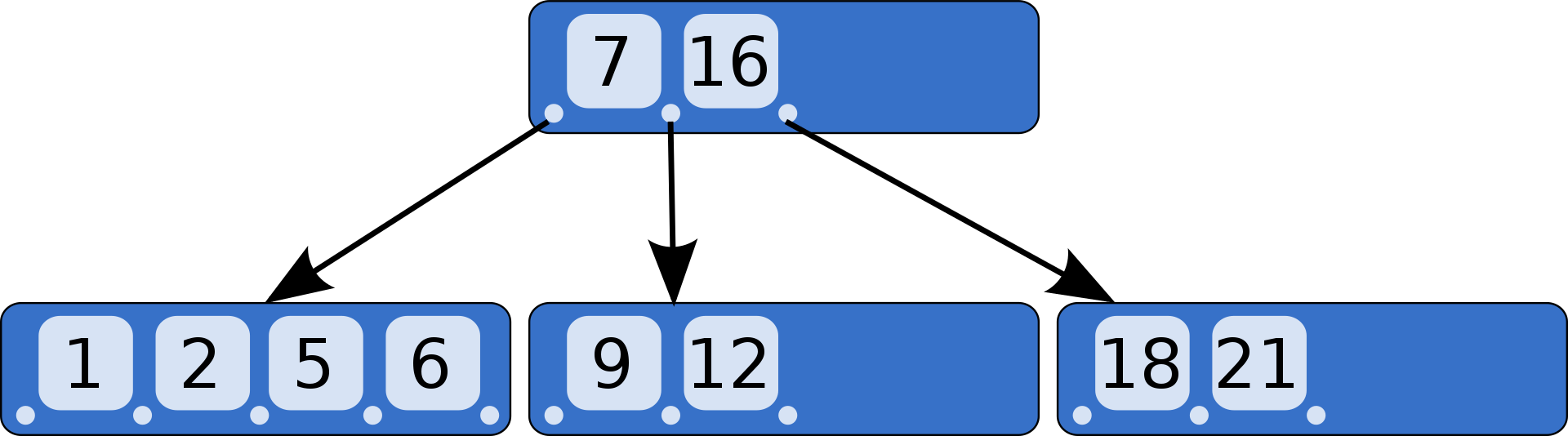
탐색
탐색은 일반적인 방식, 즉 이진 탐색 트리와 동일한 방식으로 수행된다. 루트에서 시작하여, 하향식으로 탐색 대상의 값을 구분 값과 비교하며 자식 포인터를 찾아나가는 과정으로 진행한다.
삽입
부적절한 상태에 있는 노드란, 그 노드에 허용된 자식 노드의 숫자가 허용된 범위 밖인 노드를 의미한다.
1. 삽입될 노드가 어느 위치로 삽입될지 찾아 해당 부모 노드에 삽입한다.
2. 부적절한 상태의 노드가 없다면, 삽입 과정을 종료한다.
3. 만약, 어떤 노드가 너무 많은 항목을 가지고 있다면, 이를 두 노드로 분리한다. 이 과정을 반복적으로 트리를 타고 올라 며 진행한다. 만약 루트 노드를 분리하였다면, 새로운 루트 노드를 만든다.
#참고
L을 허용된 자식 노드의 최소수라고 하고 U를 최대수라고 하자. 그러면, 각 노드는 항상 L과 U 사이의 자식 노드를 가지게 된다. 단, 예외로 루트 노드의 경우 2에서 U사이의 어느 수의 자식 노드도 가질 수 있다. 다른 말로, 루트 노드는 최소수에서 예외로, 자신만의 최소수 2를 가진다는 것이다. 이는 트리가 적은 수의 항목을 가지는 것을 가능하게 한다. 하나의 자식 노드를 가지는 루트 노드는 전혀 의미가 없는데, 이는 해당 자식 노드에 연결된 부트리를 직접 루트 노드에 연결하면 되기 때문이다. 자식 노드를 가지지 않은 루트 노드 역시 불필요한데, 이는 항목이 없는 트리는 일반적으로 루트 노드조차 없는 것과 같기 때문이다.
[출처: Wikipedia]
#Large Tree
트리는 데이터베이스의 전체 레코드를 저장하는 데 사용할 수 있으며, 파일에 있는 레코드 컬렉션의 메모리 내 표현으로 사용할 수 있다. 트리는 또한 레코드 모음의 인덱스를 파일에 저장하는 데 사용할 수 있다. 두 경우 모두 레코드 컬렉션이 상당히 큰 경우 트리가 너무 커서 한 번에 모든 레코드를 메모리에 저장할 수 없다. 예를 들어 230개의 레코드를 저장하는 데이터베이스 파일이 있고 각 인덱스 항목에 8바이트의 저장 공간이 필요한 경우 인덱스를 저장하는 BST에는 230개의 노드가 필요하며 각각 16바이트의 메모리(32비트 포인터) 또는 16GB의 메모리가 필요하다. 그렇기 때문에 다른 방법은 전체 트리를 디스크의 파일에 저장하고 직접 관련된 부분만 메모리에 로드하는 것이다
#디스크 표현
디스크 파일에 이진 트리를 쓰는 것은 비교적 간단한 일로, 데이터 요소를 보유한 데이터 레코드와 하위 노드의 위치를 지정하는 두 개의 파일 오프셋으로 각 트리 노드를 표현한다
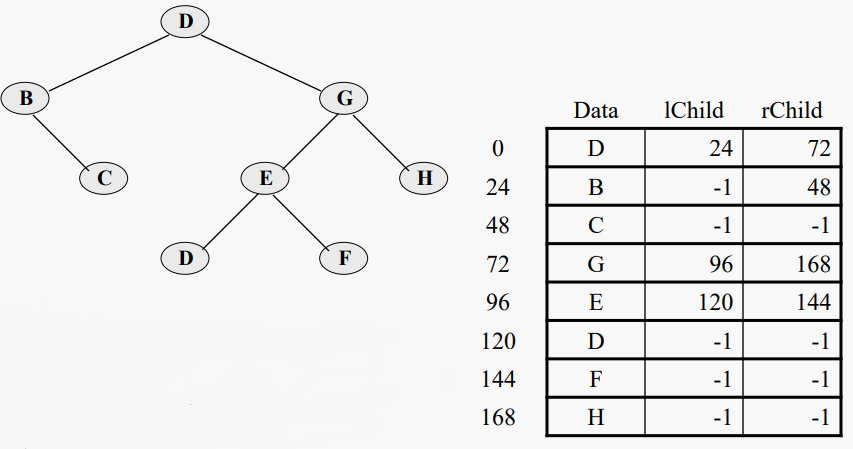
노드는 특정 순서로 저장할 필요가 없다. null 포인터는 음수 오프셋(-1)으로 나타낼 수 있다.
문제는 이 디스크 표현이 검색 또는 트래버설과 같은 일반적인 트리 작업을 처리할 때 너무 많은 개별 디스크 액세스를 필요로 한다는 것이다. 이러한 트리 작업은 일반적으로 노드에서 하위 노드 중 하나 또는 둘 모두로 전환해야 한다.
그러나 하위 노드가 상위 노드 근처에 저장될 이유는 없다(최소한 형제 노드가 인접해 있음을 보장할 수는 있지만).
각 노드는 하나의 데이터 값만 저장하고 노드는 트리 작업 중에 액세스하는 모든 노드에 대해 하나의 디스크 액세스를 수행할 수 있다. 하지만 디스크 액세스 속도가 매우 느리다는 점을 고려할 때 이는 그냥 넘어갈 수 없는 부분이다.
#B Trees
- 차수 m의 B-트리는 다음과 같은 특성을 가진 다방향 트리이다
- 리프노드가 아닌 이상, 루트가 적어도 두 개의 하위 트리를 갖는다
- ⌈m / 2⌉ ≤ k ≤ m 일때 각 루트가 아닌 노드와 리프가 아닌 노드는 k – 1 데이터 값을 보유하고 k는 하위 트리에 대한 포인터를 보유한다
- ⌈m / 2⌉ ≤ k ≤ m일때 각 리프 노드는 k – 1 데이터 값을 보유한다
- 모든 리프 노드는 같은 레벨에 있다
- 각 노드의 데이터 값은 오름차순이다
- 모든 i의 경우 첫 번째 i 하위 항목의 데이터 값이 i번째 데이터 값보다 작다
- 모든 i의 경우 마지막 m – i 하위 항목의 데이터 값이 i번째 데이터 값보다 크다
- 그래서, B-트리는 일반적으로 적어도 절반은 채워져 있고, 상대적으로 적은 수의 레벨을 가지고 있으며, 완벽하게 균형을 이루고 있다. 일반적으로 m은 상당히 클 것이다.
#B Tree 예시
차수가 5인 B-Tree 예시:

각 노드의 데이터 값에 이진 검색을 적용할 수 있기 때문에 검색 효율이 매우 높다
#B Tree 삽입
삽입은 BST와 유사한 논리를 따르며, 우리가 각 노드의 값 리스트를 검색하고 노드가 더 복잡한 limit을 따라야 하기 때문에 BST보다 더 구현하기 복잡하다. 전에도 말했듯 ⌈m / 2⌉ ≤ k ≤ m이다. 여기서 k는 노드가 가진 자식의 수이다.
BST와 기본적인 개념은 같다: 적절한 리프 노드를 검색하고 새로운 값을 추가한 다음 필요에 따라 분할하고 위로 승격시킨다.
예를 들어, W 값을 오른쪽의 B 트리에 삽입한 다음 X 값을 삽입하면 오른쪽 끝 리프가 분할되고 값 V가 루트로 승격된다. 그런 다음 값 Z를 삽입하면 루트가 분할되고 값 Q가 새 루트 노드로 승격된다

#B Tree 삽입 예시 1
만약 W를 삽입하게 되면 리프노드가 채워진다
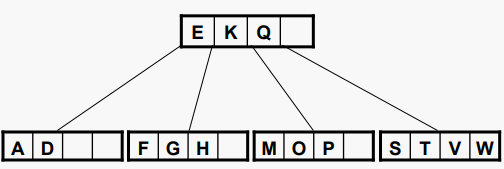
X를 삽입하면 리프가 오버플로된다. 그래서 리프노드를 쪼개서 중앙값인 V를 한 단계 올린다. 노드에 새 값을 저장할 공간이 있으므로 더 이상의 분할이 발생하지 않는다.

#B Tree 삽입 예시 2

이 경우에 I를 삽입하는 것은 두 번째 리프노드를 채우는 것이다. 그런 다음 J를 삽입하면 리프가 가득차게 된다. 그래서 리프노드를 쪼개서 중앙값인 H를 한 단계 올린다. 이제 더 삽입 시에 부모 노드가 꽉 차서 분할이 진행된다.

#B Tree 삽입 예시 3
루트를 분할하면 K가 위로 가게 된다
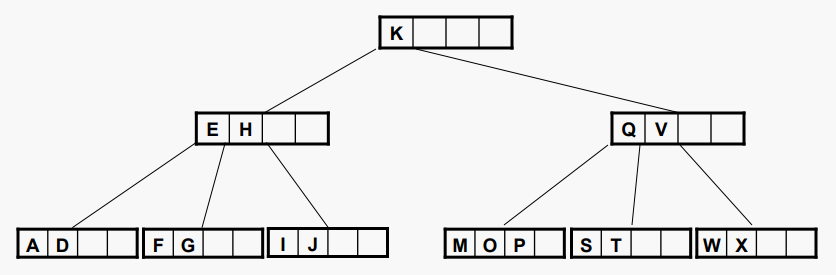
그래서, B-트리는 모든 리프 노드들을 같은 레벨로 유지하는 새로운 루트를 밀어 올림으로써 팽창한다. 여기에서 볼 수 있듯이 루트 분할은 당연히 하나의 값만 보유하는 새 루트 노드로 이어지기 때문에 루트는 하나의 값만 가지게 되기 때문에 이 경우에 다른 노드들과 다르게 2개 이상의 값을 가지고 있지 않아도 된다.
#B Tree 삽입 알고리즘
InsertHelper(Val, sRoot, upVal, upChild, splitHappened) {
NULL test, on general principles
if at leaf {
if NOTFULL {
insert Val
splitHappened = false
}
else {
split off new right sibling for sRoot
set upVal to middle value from splitting
set upChild to new right sibling
splitHappened = true
}
return
}
//find index Idx of child to descend
InsertHelper(Val, ptr[Idx], upVal, upChild, splitHappened)
. . .
if ( splitHappened ) {
if NOTFULL {
insert upVal and upChild to sRoot
splitHappened = false
}
else {
split off new right sibling for sRoot
set upVal to middle value from splitting
set upChild to new right sibling
splitHappened = true
}
}
return
}#B-Tree 탐색 비용
q = ⌈m / 2⌉ 라고 한다면, 우리는 n개의 키 값을 저장하는 B-트리의 높이에 대한 상한을 도출할 수 있다

이 값은 매우 작다. 예를 들어, m = 200이고 n = 2,000,000이면 h < = 4이다. 하지만 노드에서 데이터 값의 이진 검색을 수행하는 데 드는 비용은 적어도 log2(q)이며, 트리의 각 수준에서 이를 수행하면 총 비용은 다음과 같다:
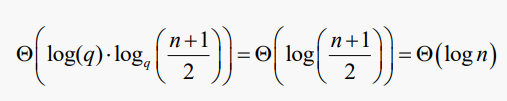
#Split 비용
삽입 비용에 대한 주요 관심사는 수행되어야 하는 분할의 수가 될 것으로 보인다(다른 모든 것은 본질적으로 BST 삽입과 유사하다). n이 증가함에 따라, 분할의 평균 확률은 다음과 같이 근사된다는 것을 보여줄 수 있다
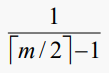
예를 들어, m = 100이면 분할 확률은 약 2%이다. 이는 예상할 만한 결과이다. 노드 분할은 노드의 데이터 값의 약 절반을 새 위치로 이동해야 하기 때문에 상당히 비용이 많이 들지만 일반적인 B-트리의 경우 그렇게 자주 필요하지 않다
#B-Tree Deletion / 삭제
노드에서 값을 삭제하는 것은 꽤나 복잡하다. 왜냐하면 자식 개수는 노드의 값 개수와 관련이 있기 때문이다.
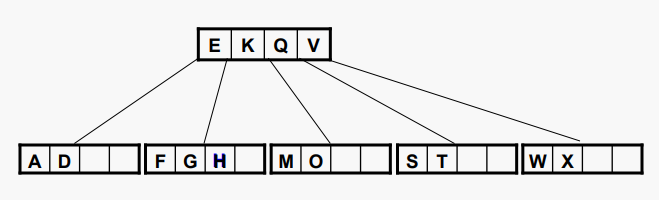
리프 노드의 경우 값을 삭제하면 필수 플로어 아래 노드의 데이터 값 수가 감소할 수 있다. 이 경우 리프 노드는 인접한 형제 노드에서 값을 빌리거나 인접한 형제 노드와 병합해야 한다. 그러나 후자는 부모 노드의 자식 수를 감소시키므로 부모 노드에서 병합된 리프로 값을 이동해야 한다. 아래 차수가 5인 B 트리에서 T를 삭제하는 것을 보자:
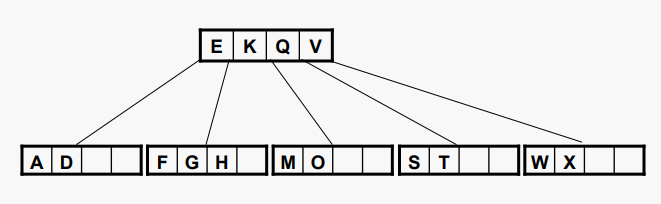
#리프노드에서 삭제
리프노드에서 T를 제거하면 그 리프노드가 "언더플로" 된다.

이렇게 되면 4번째 리프노드에 값이 하나밖이 없기 때문에 다른 형제 노드에서 값을 빌려와야한다. 하지만 두개의 형제 노드 모두 값이 2개므로 값을 빌려줄 수 없다. 그렇기 때문에 하나의 형제 노드와 병합 해야한다.

#내부 노드에서 삭제
내부 노드에서 값을 삭제하려면 값을 위의 경우로 축소 시킨다. Vk를 우리가 삭제할 값이라고 가정해보자.
리프 노드에 있어야 하는 Vk의 바로 이전 값은 삭제되는 값을 대체하기 위해 차용된 다음 리프 노드에서 삭제된다.
차수가 5인 다음 B-트리에서 K를 삭제하는 것을 보자:
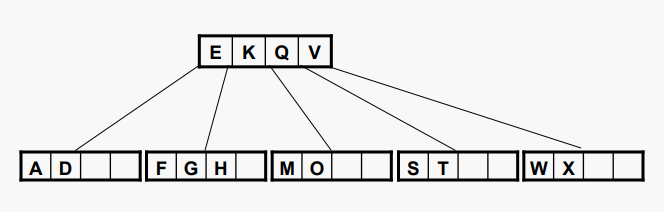
K의 전임값은 K의 왼쪽에 있는 자식노드 아래의 가장 오른쪽 리프에서 가장 큰 값이다. 이전의 값은 삭제된 값을 대체하기 위해 복사된 다음 리프에서 제거된다 (이번 경우는 비교적 간단하다).
#B Tree 삭제 알고리즘
DeleteHelper(Val, sRoot, underflowHappened) {
NULL test, on general principles
search sRoot for Val or closest predecessor
if Val does not occur in sRoot {
DeleteHelper(Val, appropriate child, underflowHappened)
if success and underflowHappened {
if can borrow {
borrow value from appropriate child
}
else {
merge appropriate children
adjust sRoot to account for merge
set underflowHappened
}
}
return
}
else if sRoot is a leaf {
delete Val from sRoot
set underflowHappened
return
}
. . .
else {
replace Val in sRoot with closest predecessor
DeleteHelpher(closest predecessor, left subtree from Val,
underflowHappened)
if success and underflowHappened {
if can borrow {
borrow value from appropriate child
}
else {
merge appropriate children
adjust sRoot to account for merge
set underflowHappened
}
}
return
}
return
}#B 트리 스토리지 효율성
- B 트리에서는
- 노드는 (기본적으로) 50% 이상 가득 차야 한다
- 또한 노드가 50%만 채워져 노드의 데이터 공간 절반을 낭비할 수 있다
- 하지만 그 "확장"된 공간은 향후 삽입을 위해 사용할 수 있다
- 여러 분석/연구와 시뮬레이션은 일반적인 사용에서 B 트리가 약 70% 가득 찰 것임을 나타낸다
- 이러한 낭비된 공간때문에 B 트리에서 여러 변형된 자료구조들이 있다
#B* Tree
- B* 트리에서는
- 루트를 제외한 모든 노드는 1/2이 아닌 2/3 이상이 채워져야 한다
- 분할은 2개의 노드를 2개의 노드로 변환하는 것이 아니라 3개의 노드로 변환한다
- 분석에 따르면 B* 트리의 평균 활용률은 약 81%이다. 앞서 말했듯 이는 70%인 B-tree보다 더 높은 수치이다
- (n+1)/(n+2)의 충전율(fill factor)을 지정하도록 일반화할 수 있다; B^n 트리
#B+ Tree
- B+ 트리에서는
- 내부 노드는 키 값과 포인터만 저장한다*.
- 모든 레코드 또는 레코드에 대한 포인터는 리프노드에 저장된다.
- 일반적으로 리프는 키 값과 오프셋을 저장하는 데이터베이스 파일 인덱스의 논리 블록일 뿐이다. 이 경우 많은 키 값이 트리에서 두 번, 검색을 안내하는 내부 노드에서 한 번, 그리고 리프에서 다시 발생한다.
- 리프노드가 단순한 인덱스인 경우, 리프노드의 레벨을 B 트리 노드의 linked list로 구현하는 것이 일반적이다
- B+ 트리는 B 트리의 가장 일반적으로 구현되는 변형이며, 대규모 데이터베이스를 위해 많이 선택되는 구조이다. 소규모 데이터베이스에서는 노드가 레코드를 저장하는 직접 데이터 구조로 B 트리를 사용하는 것이 일반적이다.
#B 트리 구현
B 트리 인터페이스 예시:
template <typename T> class BTreeT {
public:
BTreeT(unsigned int Order = 3);
~BTreeT();
// some public fns not shown
bool Insert(const T& Val);
bool Delete(const T& Val);
void Display(ostream& Out) const;
T* const Find(const T& Target);
const T* const Find(const T& Target) const;
private:
unsigned int Order;
BNodeT<T>* Root;
// some helper fns not shown
};차수는 생성자를 통해 제공되지 않고 type이 아닌 템플릿 매개 변수로 제공될 수 있지만, 그러면 B 트리를 선언할 때 로컬 변수를 사용할 수 없으므로 여기에 표시된 접근 방식은 클라이언트 관점에서 더 유연하다.
#B 트리 노드 구현
- B 트리 노드 구현은 꽤나 많은 요구사항들이 있다
- 노드는 order - 1 데이터 값을 저장할 수 있는 방법을 제공해야 한다
- 노드는 Order 포인터를 저장하는 방법을 제공해야 한다
- 노드는 데이터 값의 이진 검색을 지원해야 하므로 동적으로 할당된 배열이 적절하다
- 노드는 필요한 검색 기능과 데이터 값을 제거하고 추가하는 기능(필요에 따라 포인터 배열을 조정)을 제공해야 한다
- 노드 destructor는 어레이를 없애야 한다
- 노드는 isFull() 함수를 제공해야 하며, 언더플로와 같은 다른 테스트를 제공하거나 노드가 빌릴 수 있는 추가 값을 가지고 있는지 여부를 제공해야 한다
- B 트리 구현에 필요한 분할 및 병합 작업은 노드의 책임이 될 수 있다
- 리프 노드는 포인터가 필요하지 않기 때문에 두 개의 별개의 노드 타입을 갖는 경우가 있다. 그렇게 하면 메모리(또는 디스크 공간)를 절약할 수 있다.
가장 일반적인 접근법은 데이터 값을 저장하기 위해 크기가 order – 1인 배열을 사용하고, dimension order의 다른 배열을 사용하여 포인터를 저장한다. 두 어레이를 하나로 통합하여 데이터/포인터 쌍을 저장함으로써 데이터 값을 삽입하고 제거할 때 필요한 이동을 단순화할 수 있다. 예:
template <typename T> class Pair {
public:
T Data;
BNodeT<T>* Right;
// some members perhaps not shown
};그러면 노드는 0번째 셀을 사용하여 (맨 왼쪽의 아래에) 포인터만 저장하는 dimension order의 pair 개체 배열을 저장할 수 있다. 이 접근 방식 또한 노드를 분할할 때 일부 문제를 단순화 한다. 하지만, 이 구현은 문법상 꽤나 복잡하고 헷갈릴 수 있다.
#디스크의 B 트리 노드
물론 노드를 디스크에 영구적으로 저장하는 것이 핵심이다. 그러면 파일에 노드를 어떻게 배치할까? 여러가지 방법이 있다
- 번갈아 가며 포인터(offset)와 데이터 값을 참조
- 키 값을 블록으로 쓰고 포인터를 블록으로 쓰기
- 어떤 다른 값들이 필요한가 확인
여러 가지 옵션이 있기 때문에. 어떤 것을 선택하는 지는 사용자에게 달려있다. 물론 데이터 값의 특성도 고려해야 한다.
- 고정된 길이 단순 데이터 값인지?
- 가변 길이 또는 복잡한 데이터 값
- 텍스트 형식 또는 이진 형식?
'Computer Science > Data Structures & Algorithms' 카테고리의 다른 글
| [Lecture 15] Graph Traversal / 그래프 운행법 (0) | 2023.01.15 |
|---|---|
| [Lecture 14] Graph / 그래프 (0) | 2023.01.15 |
| [Lecture 7] 점근(asymptotic) 표기법/ Big-O 표기법 (1) | 2023.01.06 |
| [Lecture 6] Algorithm Analysis / 알고리즘 분석 (1) | 2023.01.05 |
| [Lecture 4] Hash Function / 해시 함수 (1) | 2023.01.03 |



