#Graph Traversal
그래프 운행법, 그래프 트래버설 또는 그래프 순회란 그래프를 구성하는 모든 정점들을 체계적으로 방문하는 방법이다. 큐를 이용한 넓이 우선 탐색 방법과 스택을 이용한 깊이 우선 탐색 방법이 있다. 또 부모 노드를 먼저 검사하고 왼쪽 노드에서 오른쪽 노드의 순으로 방문하는 방법인 전위 운행법과 왼쪽 노드, 부모 노드, 오른쪽 노드의 순으로 방문하는 방법인 중위 운행법, 왼쪽 노드에서 오른쪽 노드의 순으로 방문한 후 부모 노드를 검사하는 방법인 후위 운행법이 있다.
[네이버 지식백과] 그래프 운행법 [graph traversal]
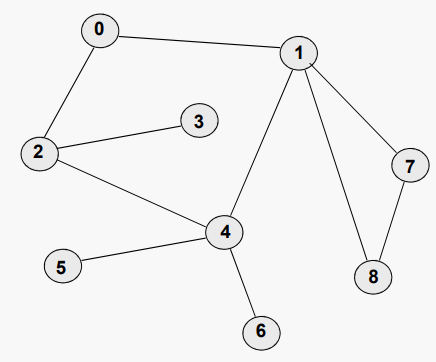
일부 알고리즘은 그래프의 모든 정점을 정확히 한 번 방문해야 한다.정점이 방문되는 순서는 중요할 수 있으며 특정 알고리즘에 따라 달라질 수 있다. 이 알고리즘 중 가장 흔한 두 가지는 위에서 언급한 depth-first (깊이 우선 탐색) 와 breath-frist (넓이 우선 탐색)이 있다. 트래버설 동안 우리는 어떤 정점이 방문되었는지 추적해야 한다; 가장 일반적인 접근법은 일종의 "표시" 할 수 있는 기능을 제공하는 것이다.
#Depth-First Search / 깊이 우선 탐색
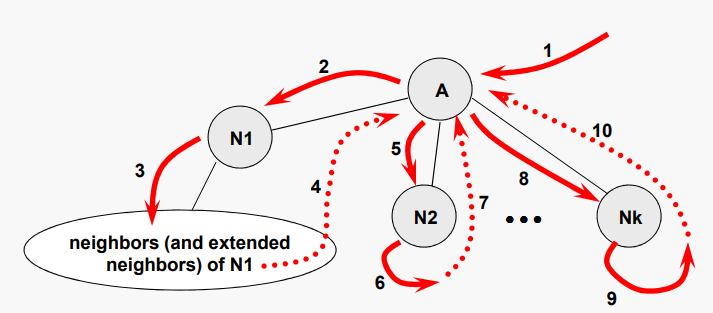
특정 노드가 시작점으로 지정되었다고 가정하자. A를 마지막으로 방문한 노드로 하고 A에 N1, N2, …, Nk의 이웃이 있다고 가정하자. 깊이 우선 트래버설은 다음을 수행한다:
N1을 방문한 다음, N1의 모든 방문되지 않은 이웃을 순회하고, 유사한 방식으로 A의 나머지 이웃을 순회한다
위의 첫 번째 예시로 나온 그래프에서 0을 시작점 이라고 가정하고 DFS를 실시하면 다음과 같은 순서로 정점을 방문한다
0 -> 1 -> 4 -> 2 -> 3 -> 5 -> 6 -> 7 -> 8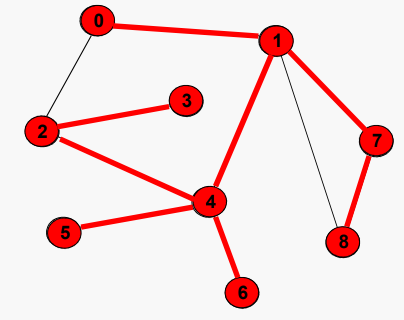
Depth-frist 트래버설 동안 취한 간선이 표시되면 그래프의 모든 노드를 표시하는 트리가 정의된다(꼭 이진 트리가 아니여도 된다). 이러한 트리를 그래프에 대한 *스패닝 트리 / 신장 트리 (spanning tree)라고 한다
*스패닝 트리란 연결 그래프의 부분 그래프로서 그 그래프의 모든 정점과 간선의 부분 집합으로 구성되는 트리. 모든 노드는 적어도 하나의 간선에 연결되어 있어야 한다. 더 자세히 말해 연결된, 비방향성 그래프 G에서 순환 경로를 제거하면서 연결된 부분 그래프가 되도록 이음선을 제거하면 스패닝 트리가 된다. 따라서 스패닝 트리는 G 안에 있는 모든 정점을 다 포함하면서 트리가 되는 연결된 부분 그래프이다.
#Depth-First Traversal 구현 예시
public static void DFS(AdjMatrix G, int Start) {
G.Mark(Start);
for (int w = G.firstNeighbor(Start); G.hasEdge(Start, w); w = G.nextNeighbor(Start, w) ) {
if ( !G.isMarked(w) ) {
DFS(G, w);
}
}
}위 코드를 첫 번째 예시에 적용하면 다음과 같이 그래프를 순회한다:
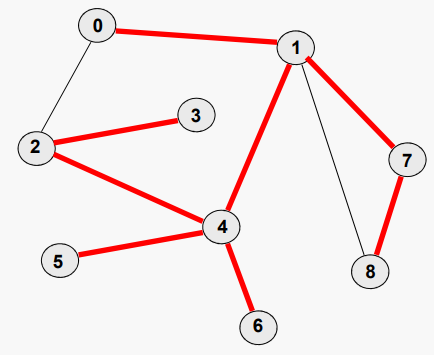
DFS()를 수정하여 다른 AdjMatrix 오브젝트를 매개 변수로 취하는 경우 DFS()가 스패닝 트리의 copy를 만들도록 하는 것은 상대적으로 어렵지 않다.
#Breath-First Search / 넓이 우선 탐색
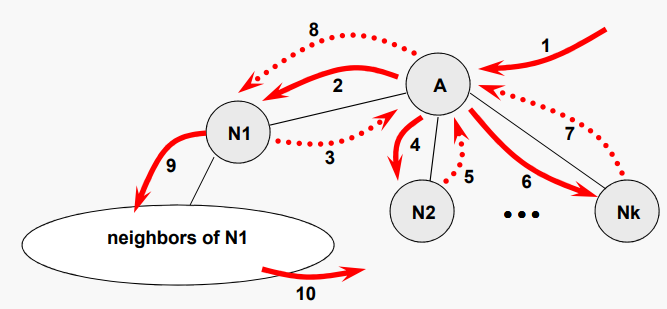
특정 노드가 시작점으로 지정되었다고 가정하자. A를 마지막으로 방문한 노드로 설정하고 A에 N1, N2, …, Nk의 인접 노드가 있다고 가정하자. 넓이 우선 탐색은 다음을 수행한다:
N1을 방문한 다음 N2를 통해 Nk를 순회한 다음 N1의 모든 방문되지 않은 바로 이웃을 순회하고 N2 와Nk의 바로 이웃을 유사한 방식으로 순회한다.
첫 번째 예시의 그래프에서 BFS를 실행하면 다음과 같은 순서로 정점을 방문한다
0 -> 1 -> 2 -> 4 -> 7 -> 8 -> 3 -> 5 -> 6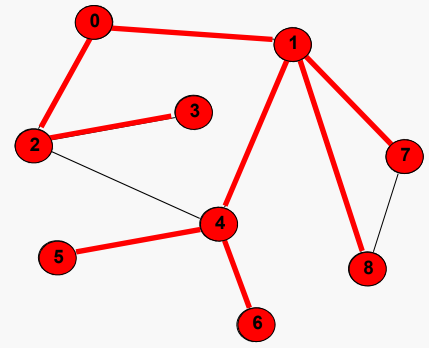
넓이 우선 탐색 중에 취한 간선은 지정된 그래프에 대한 스패닝 트리도 정의한다. 여기에서와 같이 Breath-first 스패닝 트리는 일반적으로 Depth-frist 스패닝 트리와 다르다.
#Breath-First Traversal 구현 예시
너비 우선 통과는 로컬 대기열(queue)을 사용하여 그래프 노드를 적절한 순서로 구성한다
public static void BFS(AdjMatrix G, int Start) {
LinkedList<Integer> toVisit = new LinkedList<Integer>();
toVisit.addLast(Start);
G.Mark(Start);
while ( !toVisit.isEmpty() ) {
int VisitNow = toVisit.removeFirst();
for (int w = G.firstNeighbor(VisitNow); G.hasEdge(VisitNow, w); w = G.nextNeighbor(VisitNow, w) ) {
if ( !G.isMarked(w) ) {
toVisit.addLast(w);
G.Mark(w);
}
}
}
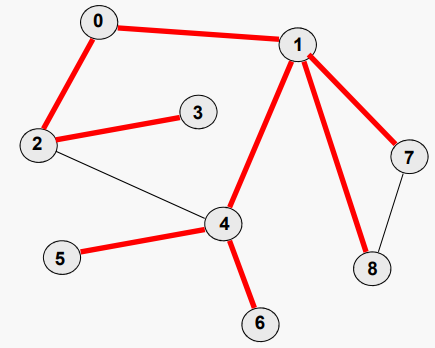
}for 루프는 향후 방문을 위해 현재 노드의 모든 방문되지 않은 이웃을 schedule한다. 위 코드를 첫 번째 예시에 적용하면 다음과 같이 그래프를 순회한다:
'Computer Science > Data Structures & Algorithms' 카테고리의 다른 글
| [Lecture 18] Sorting Algorithm / 정렬 알고리즘 (0) | 2023.01.16 |
|---|---|
| [Lecture 16] Weighted Graph / 가중 그래프 (0) | 2023.01.15 |
| [Lecture 14] Graph / 그래프 (0) | 2023.01.15 |
| [Lecture 13] B-Tree / B-트리 (0) | 2023.01.12 |
| [Lecture 7] 점근(asymptotic) 표기법/ Big-O 표기법 (1) | 2023.01.06 |



