#Graph
그래프는 꼭짓점과 변의 집합을 이루는 순서쌍을 의미하며, 관계를 간선과 정점으로 표현한 구조이다. 간선으로 연결한 두 정점을 '인접(Adjacent)해 있다' 혹은 '이웃 관계'라고 표현하며, 그래프에서 정점들이 연결된 다양한 노선을 경로라고 표현한다.
쉽게 말해 데이터의 원소에 해당하는 정점(Vertex)과 정점간의 관계를 간선(Edge)으로 연결하여 표현한 형태의 자료구조이다. 일반적으로 정점은 원으로 표현하고 변은 화살표나 선분으로 표현한다. 변을 화살표로 나타내는 경우에는 해당 방향으로만 이동할 수 있으며, 이러한 그래프를 유향 그래프(Directed graph)라고 말한다. 반대로 선분으로 표현되는 경우에는 양방향 모두 이동이 가능하며, 이러한 그래프를 무향 그래프(Undirected graph)라고 말한다. 그리고 변의 경우에는 특정한 수치를 가질 수 있는데 이를 가중치(Weighted value)라고 말한다.
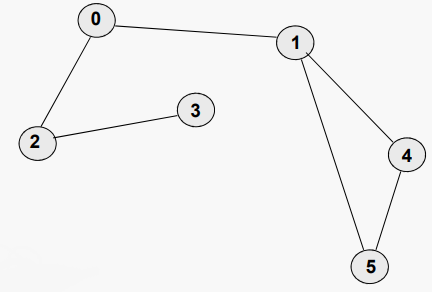
예를 들어 도시를 정점으로 생각하고 도시 사이를 잇는 도로를 변으로 생각하면 그래프는 곧 하나의 간략화된 지도가 된다. 위의 그림에서 1~6번 원이 도시고 연결선이 도로인 셈. 여기에 각 도로마다 도로의 길이 또는 이용 요금을 써 넣으면 이것이 바로 그 도로의 가중치이다.
위에서 알 수 있듯이 그래프는 도시와 도로로도 비유될 수 있기 때문에 두 지점 간의 최단 경로(또는 가장 저렴한 경로)를 구하는 데 널리 이용된다. 그래프는 도시-도로뿐만 아니라 컴퓨터 통신망, SNS에서의 친구관계 등등 여러 상황을 모델링 할 수 있어 많은 분야에서 널리 사용된다. 예를 들어 어떤 웹 페이지를 정점으로 하고 페이지에 달린 링크들을 다른 페이지로 가는 변이라고 보면, 나무위키 역시 하나의 거대한 그래프라고 볼 수 있다.
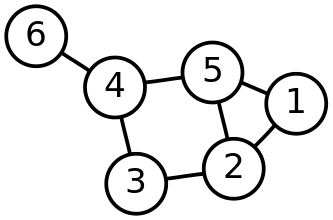
위의 그림에서는 2,3,4,5번 도시(정점)들이 서로 연결되어 순환할 수 있다. 다시 말해서 2번 도시에서 출발하여 3,4,5번 도시를 거쳐 다시 2번에 도착할 수 있다는 것. 이와는 반대로, 이렇게 순환하지 않는 그래프를 트리(그래프)라고도 부른다.
순수수학에서는 수학자 레온하르트 오일러가 한붓그리기 문제, 즉 쾨니히스베르크 다리 건너기 문제를 푼 것을 그래프 이론의 시작으로 보고 있다. 이 외에도 그래프 이론에서 대중에게 비교적 친숙한 문제로는 4색정리나 해밀턴 회로[1] 등이 있을 것이다.
그래프의 유형
· 무방향성 그래프(Undirected Graph) : 방향성이 없는 그래프로, (A, B) = (B, A)이다.
· 방향성 그래프(Directed Graph) : 방향성을 가지고 표현한 그래프로, (A, B) ≠ (B, A)이다.
· 가중치 그래프(Weighted Graph) : 간선에 가중치를 할당한 그래프이다.
그래프의 탐색
그래프는 연결된 정점을 탐색하는데 크게 두 가지 탐색 방법이 있다.
· DFS(Depth First Search) : 시작 정점부터 더 이상 길이 안 보일 때까지 탐색하는 깊이 우선 탐색 방법이다.
· BFS(Breadth First Search) : 시작 정점부터 옆으로 좌우로 탐색하는 너비 우선 탐색 방법이다.
그래프 G는 정점의 집합 V와 V와 구별되는 정점의 쌍의 집합 E로 구성된다. 이러한 정점 쌍을 간선 / edge이라고 한다. 정점 쌍이 순서가 없으면 G는 무방향 그래프이다. 정점 쌍이 순서대로 정렬되어 있다면, G는 방향성 그래프 또는 digraph이다.
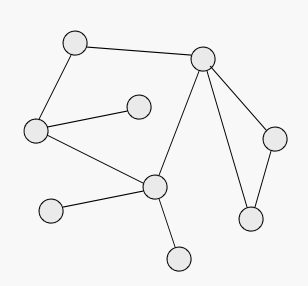
#무방향 그래프 용어
V = {a, b, c, d, e, f, g, h, i} a i g f e d c b h
E = { {a, b}, {a, c}, {b, e}, {b, h}, {b, i} , {c, d} , {c, e} , {e, f} , {e, g} , {h, i} }
인 무방향 그래프가 있을때
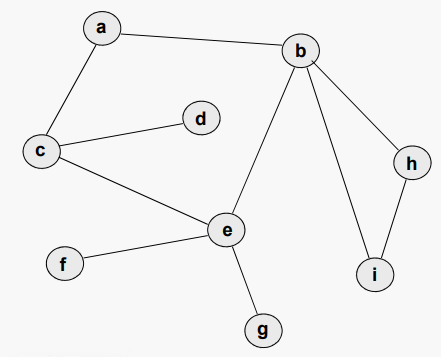
e = {c, d}는 정점 c와 d에 "부속 (incident)"하는 간선이다. {x, y}가 edge(E)인 경우 두 정점 x와 y가 인접(adjacent)하다
G에서의 경로는 각각 다음에 인접한 별개의 정점들의 시퀀스이다. 경로에서 같은 정점이 두 번 발생하지 않는 경우 경로는 단순 (simple) 하다고 한다.
G에서의 순환(cycle)은 G에서의 경로이며, 적어도 세 개의 정점을 포함하고 있고, 마지막 정점이 첫 번째 정점에 인접해 있다.
G에서 두 정점 x와 y가 주어지면 G에 첫 번째 정점 x와 마지막 정점 y를 가진 경로가 있으면 그래프가 연결되었다고 한다.
그렇기 때문에 우리가 위에서 본 그래프도 연결그래프이다.
그래프 G가 연결되어 있지 않다면, 우리는 정점의 최대 연결 집합이 G의 요소(component)라고 말한다
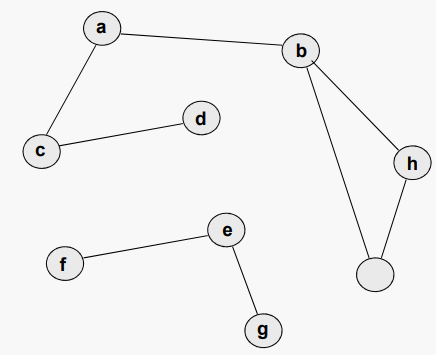
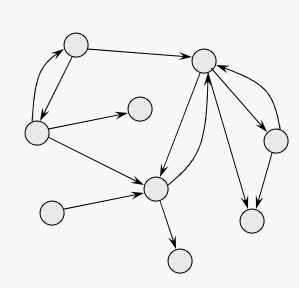
#방향성 그래프 용어
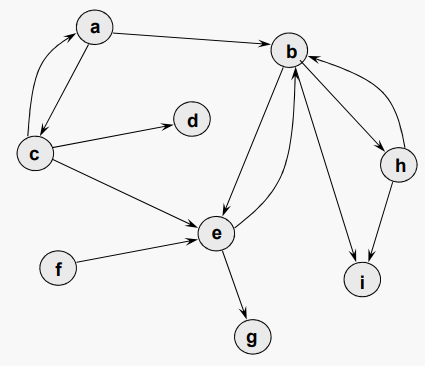
방향성 그래프에 쓰이는 용어들도 무방향 그래프 용어들과 크게 다르지 않다.
e = (c, d)는 c에서 d까지의 간선이다. 방향성 그래프 G에서 방향 경로는 각각의 정점에서 다음 정점까지의 edge 있는 별개의 정점의 시퀀스이다.
방향 그래프 G는 G의 간선의 방향을 억제하여 얻은 무방향 그래프가 (이전의 정의에 따라) 연결되어 있으면 weakly conneceted 되었다고 한다.
방향 그래프 G는 G에서 두 정점 x와 y가 주어지면 x에서 y까지의 방향 경로가 G에 있을 때 strongly conneceted 되었다고 한다.
#인접 행렬 / Adjacency Matrix로 그래프 표현
인접행렬이란 그래프의 구조를 표현하기 위해 정점 수만큼의 열과 행을 가진 행렬을 이용하는 방법을 말한다. 정점 i와 j 사이에 간선(edge)이 있으면 i번째 행과 j번째 열의 원소가 1, 그렇지 않으면 0으로 표시된다. 쉽게 말해 각 정점들 간의 연결 상태를 행렬과 같은 형태로 나타내는 방법이다. 정점의 개수가 n개일 때 인접 행렬 M은 n×n의 정사각 행렬 형태를 띤다. i행, j열의 값이 1이면 i와 j에 해당하는 정점이 인접해 있는 것이고, 그 값이 0이면 인접하지 않은 것이다. 예를 들어 3행, 2열의 값이 1이면 3행에 해당하는 정점 C와 2열에 해당하는 정점 B가 인접해 있다는 것을 표현한다. 비용 인접 행렬은 최단 경로를 찾기 위한 가중치를 표시한 그래프를 인접 행렬로 나타낸 것으로, 비용 인접 행렬 Cost(i, j)는 Vi로부터 Vj로의 가중치를 나타내며, ∞은 존재하지 않음을 의미한다. 0은 Vi=Vj인 경우이다.
[네이버 지식백과] 인접 행렬 [adjacency matrix]
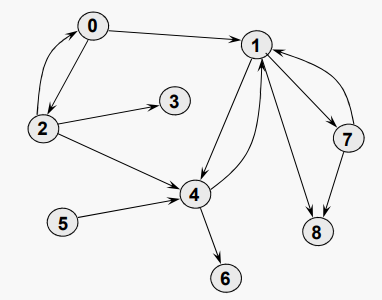
그래프는 2차원 인접 행렬로 표현될 수 있다. 만약 G가 n개의 = |V| 꼭짓점을 갖는다면, M은 다음과 같이 정의되는 n개의 n개의 행렬이라고 하자
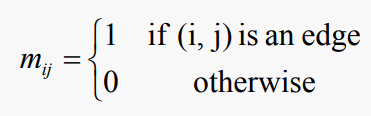
그렇다면 위의 그래프는 다음과 같은 인접 행렬로 표현될 수 있다.

- 인접 테이블은:
- 특정 에지의 존재 여부를 결정하기 위해 θ(1) 필요
- θ( |V|^2)스토리지 비용(유형 변경으로 비용 75% 이상 절감)
- 특정 꼭짓점에서 접근 가능한 모든 꼭짓점을 찾기 위해 θ( |V| ) 필요
- edge 추가 또는 삭제 비용은 θ(1)
- 정점을 추가하거나 삭제하기가 쉽지 않으며 정적 그래프 구조에 더 적합하다.
- 무방향 그래프에 대한 대칭 행렬이므로 절반은 중복된다

#인접 테이블 / Adjacency Table로 표현
약간 다른 접근법은 인접 테이블을 사용해 구조에서 인접한 노드만 나타내는 것이다


#인접 리스트/ Adjacency list로 표현
인접 리스트 구조는 단순히 인접 테이블의 연결된(linked) 버전이다
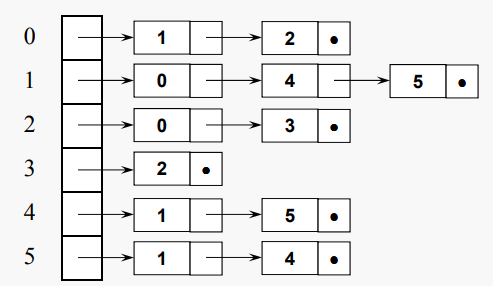
Linked list의 배열이다. 여기서 리스트 노드는 이웃에 대한 노드 레이블을 저장한다
- 인접 리스트 구조는:
- 최악의 경우: 특정 edge의 존재를 결정하는 비용은 θ( |V| )
- θ( |V| + |E| ) 저장 비용
- 최악의 경우: 특정 정점의 모든 이웃을 찾기 위한 비용은 θ( | V| )
- 최악의 경우: 가장자리를 추가하거나 삭제하려면 θ( |V| )
- 정점을 추가하거나 삭제하는 것은 여전히 쉽지 않지만 배열 대신 연결 리스트를 사용할 수 있다.
- 무방향 그래프의 경우 가장자리 수에 대한 상한은 다음과 같다. |E| ≤ |V|*(|V|-1). 따라서 인접 행렬 체계와의 공간 비교는 쉽지 않다
#인접 행렬 클래스
public class AdjMatrix {
private int numVertices;
private boolean[] Marker; // used for vertex marking
private int[][] Edge; // Edge[i][j] == 1 iff (i,j) exists
public AdjMatrix(int numV) {...}
public boolean addEdge(int Src, int Trm) {...}
public boolean delEdge(int Src, int Trm) {...}
public boolean hasEdge(int Src, int Trm) {...}
public int firstNeighbor(int Src) {...} //firstNeighbor()는 Src에 인접한 첫 번째 정점을 반환.
public int nextNeighbor(int Src, int Prev) {...} //nextNeighbor()는 Src에 인접한 Prev 뒤의 다음 정점을 반환
public boolean isMarked(int V) {...}
public boolean Mark(int V) {...}
public boolean unMark(int V) {...}
public void Clear() {...} // erase edges and vertex marks
public void Display() {...}
}'Computer Science > Data Structures & Algorithms' 카테고리의 다른 글
| [Lecture 16] Weighted Graph / 가중 그래프 (0) | 2023.01.15 |
|---|---|
| [Lecture 15] Graph Traversal / 그래프 운행법 (0) | 2023.01.15 |
| [Lecture 13] B-Tree / B-트리 (0) | 2023.01.12 |
| [Lecture 7] 점근(asymptotic) 표기법/ Big-O 표기법 (1) | 2023.01.06 |
| [Lecture 6] Algorithm Analysis / 알고리즘 분석 (1) | 2023.01.05 |



