#Heap 이란
컴퓨터의 기억 장소에서 그 일부분이 프로그램들에 할당되었다가 회수되는 작용이 되풀이되는 영역. 스택 영역은 엄격하게 후입 선출(LIFO) 방식으로 운영되는 데 비해 히프는 프로그램들이 요구하는 블록의 크기나 요구/횟수 순서가 일정한 규칙이 없다는 점이 다르다. 대개 히프의 기억 장소는 지시자(pointer) 변수를 통해 동적으로 할당받고 돌려준다. 이는 연결 목록이나 나무, 그래프 등의 동적인 자료 구조를 만드는 데 꼭 필요한 것이다.
쉽게 말해 여러 개의 값 중에서 가장 크거나 작은 값을 빠르게 찾기 위해 만든 이진 트리이다. 짧게 힙(Heap)이라고 줄여서 부른다
영단어 힙(heap)은 '무엇인가를 차곡차곡 쌓아올린 더미'라는 뜻을 지니고 있다. 힙은 항상 완전 이진 트리의 형태를 띠어야 하고, 부모의 값은 항상 자식(들)의 값보다 크거나(Max heap 최대 힙), 작아야(Min heap 최소 힙)하는 규칙이 있다. (그러므로 사진은 최소 힙(Min head이다.) 따라서 루트노드에는 항상 데이터들 중 가장 큰 값(혹은 가장 작은 값)이 저장되어 있기 때문에, 최댓값(혹은 최솟값)을 O(1)안에 찾을 수 있다.
단순히 최댓값(최솟값)을 O(1)안에 찾기 위해서라면 "항상 완전 이진 트리의 형태여야 한다"는 조건을 만족시킬 필요는 없다. 완전 이진 트리를 사용하는 이유는 삽입/삭제의 속도 때문이다. 물론 '힙 트리'는 정의상 완전 이진 트리를 사용하는 트리다. 달리 다른 구조를 사용한다 해도 전혀 얻을게 없는 최적의 구조이기 때문이다.
데이터의 삽입과 삭제는 모두 O(logN)이 소요된다
.
Heap은 완전 이진트리의 구조를 가지고 있기 때문에 트리의 레벨이 늘어날 수록 노드의 수는 두배씩 증가한다.
그말은 레벨이 i라고 가정했을때 i레벨의 노드수는 2^(i-1)개이다. (단 i는 마지막 레벨은 아니다. 이는 완전이진트리의 특성때문이다.) 그러므로 트리의 높이는 노드의 수를 통해서 알 수 있다. 트리의 높이는 log_2i+1에서 소수점을 버린값이다.
Heap에서 데이터의 삽입과 삭제는 이 높이와 관련이 있기때문에 빅오 표기법에 의해 O(logN)이라고 표현된다.
[네이버 / 나무위키 힙]
#Heap
힙은 완전한 이진 트리이다. 최대 힙 (max-heap)은 각 내부 노드의 값이 해당 노드의 하위 노드의 값보다 크거나 같은 완전이진 트리아다. min-heap은 max-heap의 반대이다, 즉 내부 노드의 값이 해당 노드의 하위 노드의 값보다 작거나 같은 완전 이진 트리이다.
노드가 인덱스 k에 저장되면 왼쪽 자식은 인덱스 2k+1에 저장되고 오른쪽 자식은 인덱스 2k+2에 저장된다

#Heap 만들기
힙이 완전한 이진 트리라는 사실은 단순한 배열을 사용하여 힙을 효율적으로 표현할 수 있게 한다. N개의 값들의 배열이 주어지면, 각 내부 노드들을 적절한 위치로 단순히 "sifting" 함으로써, 그 값들을 포함하는 힙을 만들 수 있다
- 마지막 내부 노드부터 시작
- 필요한 경우 현재 내부 노드를 더 큰 하위 노드와 교환
- 그런 다음 스왑된 노드를 따라 이동
- 모든 내부 노드가 완료될 때까지 계속 진행
다음 예시를 보자. 힙이 아닌 일반 이진 트리를 max-heap으로 바꿔 보자:

#Heap 클래스 인터페이스
maxheap 클래스를 한번 보자:
public class BinaryHeap<T extends Comparable<? super T>> {
private static final int DEFCAP = 10; // default array size
private int size; // # elems in array
private T [] elems; // array of elems
public BinaryHeap() { . . . } // construct heaps in
public BinaryHeap( int capacity ) { . . . } // various ways
public BinaryHeap( T [ ] items ) { . . . }
public boolean insert( T D ) { . . . } // insert new elem
public T findMax() { . . . } // get maximum element
public T deleteMax() { . . . } // remove maximum element
public void clear() { . . . } // reset heap to empty
public boolean isEmpty() { . . . } // is heap empty?
private void siftDown( int hole ) { . . . } // siftdown algorithm
private void buildHeap() { . . . } // heapify
public void printHeap() { . . . } // linear display
}#buildHeap과 siftDown
buildHeap 함수:
private void buildHeap() {
// first elem is stored at index 1, not 0
for ( int idx = size / 2; idx > 0; idx-- )
siftDown( idx );
}siftDown 함수:
private void siftDown(int hole) {
int child;
T tmp = elems[ hole ];
for ( ; hole * 2 <= size; hole = child ) {
child = hole * 2;
if ( child != size &&
elems[ child + 1 ].compareTo( elems[ child ] ) > 0 ) //어떤 하위 노드가 더 큰 노드인지 확인
child++;
if ( elems[ child ].compareTo( tmp ) > 0 )
elems[ hole ] = elems[ child ]; //자식 노드가 부모 노드보다 크면 위로 이동
else
break;
}
elems[ hole ] = tmp; //마지막으로, 시작 값을 올바른 위치에 넣는다
}위 코드에서는 최악의 경우, iteration당 두 번의 요소 비교와 한번의 요소 copy를 수행한다. 레벨 수는 N개 노드의 완전한 이진 트리에서 최대 1 + log(N)이다. 루프의 각 non-terminating 반복은 목표값을 1레벨의 거리로 이동시키기 때문에 루프는 log(N)회 이상의 반복을 수행하지 않는다. 따라서, SifeDown()의 최악의 경우 비용은 Θ(log N)이다. (이것은 2개의 로그(N) 비교와 로그(N) 스왑이다).
#buildHeap의 비용
노드가 N개인 완전한 이진 트리로 시작한다고 가정하자. 트리도 가득 차면 값을 아래로 선별하는 데 필요한 단계 수가 최대화된다. 이 경우 일부 정수 d = ⌈log N⌉에 대해 N = 2d -1이 된다. 예를들면

레벨 0: 2^0 노드가 아래로 sift 가능함 d - 1 level
레벨 1: 2^1 노드가 아래로 sift 가능함 d - 2 level
레벨 2: 2^2 노드가 아래로 sift 가능함 d - 3 level
우리는 일반적으로 완전하고 완전한 이진 트리의 레벨 k는 2k개의 노드를 포함하며, 이러한 노드들은 잎보다 d – k – 1레벨 위에 있다는 것을 증명할 수 있다. 따라서 최악의 경우 N개의 노드 힙을 구축하는 데 필요한 비교 수는 다음과 같다:
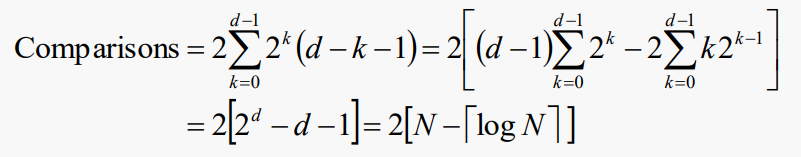
최악의 경우 두 비교마다 이동이 하나씩 있기 때문에 요소 이동의 최대 수는 N – ⌈log N⌉ + 1이다.
따라서 N개의 노드 힙을 구축하는 것은 비교와 요소 이동 모두에서 Θ(N)이다.
#힙의 루트 삭제
힙에서 가장 일반적인 작업은 루트 노드를 삭제하는 것이다. 힙 property는 sifting down 되며 유지된다
public T deleteMax() {
if ( isEmpty( ) ) //heap이 비었는지 확인
throw new RuntimeException( );
T maxItem = elems[ 1 ];
elems[ 1 ] = elems[ size ];//루트 저장후(index 1에서)마지막 리프로 바꾸고 힙을 노드 하나씩 축소
size--;
siftDown( 1 );
return maxItem;
}힙 속성을 복원하려면 새 루트를 아래로 sift down한다
#루트 삭제 예시
다음과 같은 힙이 주어졌을 시 루트를 삭제해보자:

N개의 노드 힙에서 루트가 sift-down 할 수 있는 최대 거리는 ⌈log N⌉ - 1이 될 것이다.
#루트 삭제 비용
힙 구축에 대한 이전의 분석을 보면, 완전한 이진 트리의 레벨 k는 2^k개의 노드를 포함할 것이며, 이러한 노드들은 루트 레벨보다 낮은 k개의 레벨이다. 따라서 루트를 삭제할 때 스왑된 노드가 sift down 될 수 있는 최대 레벨 수는 해당 노드가 스왑된 레벨 수이다. 따라서 최악의 경우 모든 루트를 삭제하기 위해 다음과 같은 수의 비교가 필요하다:

일반적으로 힙 정렬을 사용하면 기본적으로 동일한 수의 요소 이동이 필요하다
#힙 정렬
목록은 먼저 힙에 빌드한 다음 힙이 비워질 때까지 힙에서 루트 노드를 반복적으로 삭제하여 정렬할 수 있다. 삭제된 루트가 배열에 역순으로 저장되면 오름차순으로 정렬된다(최대 힙이 사용되는 경우).
public static void heapSort(Integer[] List, int Sz) {
BinaryHeap<Integer> toSort = new BinaryHeap<Integer>(List, Sz);
int Idx = Sz - 1;
while ( !toSort.isEmpty() ) {
List[Idx] = toSort.deleteMax();
Idx--;
}
}#힙 정렬 비용
이전 분석에서 힙을 구축하는 비용을 추가하자
총 비교수:
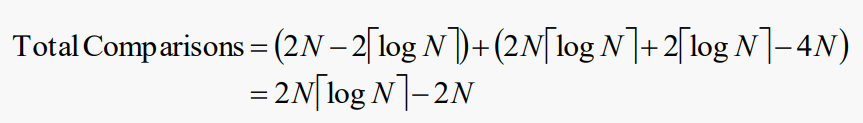
총 스왑 수:

따라서 최악의 경우 스왑과 비교 모두에서 힙 정렬의 비용은 Θ(N log N)이다
#Priority Queues
Priority Queue는 큐 데이터 구조이고 힙은 데이터를 운영하고 구성하는 트리 데이터 구조이다. Priority Queue는 priority 기능을 갖는 큐로 동작하는 큐 데이터 구조에 기초한다. 힙은 알고리즘을 사용하여 특정 순서로 데이터를 정렬하는 데 사용되는 트리 데이터 구조이다
Priority Queue는 항목으로 구성되며, 각 항목에는 항목의 priority라고 하는 키 필드가 포함된다.
creation, clearing, full 또는 empty 인지 테스트, size() 외에 Priority Queue에는 다음 두 가지 작업만 있다:
- 새 항목 삽입
- 가장 큰(또는 가장 작은) 키를 가진 항목 제거
키 값은 고유할 필요가 없다. 그렇지 않으면 가장 큰 값을 가진 항목을 제거할 수 있다
#Priority Queue 나타내기
Priority Queue의 표현은 다음과 같은 것들을 사용하여 달성될 수 있다
- 정렬된 리스트
- 정렬되지 않은 리스트
- max-heap
Priority Queue는 time-sharing environment에서 우선순위가 부여된 프로세스를 관리하는 데 사용될 수 있다
'Computer Science > Data Structures & Algorithms' 카테고리의 다른 글
| [Lecture 20] Sorting Analysis / 정렬 알고리즘 분석 (0) | 2023.01.17 |
|---|---|
| [Lecture 18] Sorting Algorithm / 정렬 알고리즘 (0) | 2023.01.16 |
| [Lecture 16] Weighted Graph / 가중 그래프 (0) | 2023.01.15 |
| [Lecture 15] Graph Traversal / 그래프 운행법 (0) | 2023.01.15 |
| [Lecture 14] Graph / 그래프 (0) | 2023.01.15 |



